陶哲軒轉發、菲爾茲獎得主領銜:AI正在顛覆數學家的工作方式

陶哲軒按讚轉發,《美國數學學會通報》用一整期特刊介紹了AI為數學帶來的改變。
這些文章讀起來很有趣,儘管使我自己即將發表的一篇文章顯得多餘……這個領域發展太快了!
作者陣容非常豪華,包括菲爾茲獎得主Akshay Venkatesh、華裔數學家鄭樂雋、電腦科學家Ernest Davis等多位知名學者。
其中鄭樂雋表示,如果最終機器能做得比人類更好,那就很好,她將樂意退出數學領域去彈鋼琴。
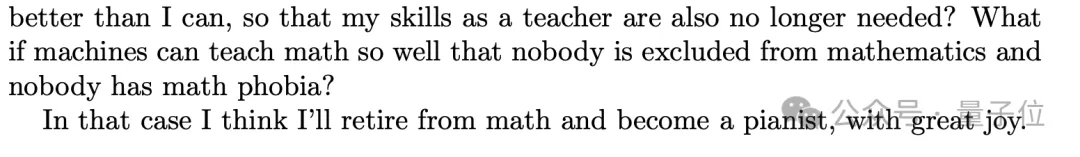
他們提出的觀點包括:
- AI的數學能力不完全反映人類的認知過程,依賴訓練資料中的模式,而不是真正理解問題的本質。
- 合成數學如合成拓樸學和合成微分幾何學,提供了一種全新的數學實踐方式,讓數學家專注於更深層的概念和問題。
- 互動式證明系統與軟體工程中的“規範驅動開發”,可以降低數學家的認知負荷、促進數學家之間的合作。
- 形式化證明科技可能改變數學證明的本質、顛覆數學家的工作方式。
- 數學屆不應被科技公司主導的議程所綁架。

在開篇,編委會寫道:
純粹的數學家習慣於享有很大程度的研究自主和智力自由,這是一種脆弱而寶貴的遺產,可能會因機器的盲目使用而被掃除。
另一方面,對同一技術進行深思熟慮和深思熟慮的方法可能會極大地豐富我們的學科。
學科應該如何發展是由我們自己決定的,因此我們邀請數學界認真思考和討論專刊中提出的問題,並聆聽其他領域同行對這些問題進行了深入思考。
現在,是數學家們了解並推動這場辯論,並決定學科未來方向的時候了。
AI能自動證明定理嗎?
計算機已經在數學中發揮了重要作用,尤其是在計算效率方面的提升,但是否能夠幫助人類進行數學推理?有一天它們是否會自主進行推理?

數學家Kevin Buzzard概述了神經網路、電腦定理證明器和大型語言模型的最新發展。
Kevin Buzzard現任英國倫敦帝國學院數學教授,專門研究算術幾何和朗蘭茲綱領。

回顧整個計算工具的歷史,最早Computer一詞還指人類作為“計算員”,他們的成就不應被低估。
17世紀早期,蘇格蘭數學家John Napier建構了第一個對數表,他提出如果有更多「計算員」來幫忙,就可以進一步推進這項工作。
另一個代表性成果是Felkel和Vega在18世紀70年代發表的整數因式分解表,這使得研究素數分佈成為可能,最終導致了素數定理的證明。
早期電子計算機出現後,機器在高速運算方面已經遠超人類,Computer一詞的意思也改變了。
如劍橋大學在1957年購買了EDSAC II計算機,用於海洋學計算,為現代板塊構造理論奠定基礎。
這個階段計算機還只是一個工具,即使目前的計算機也難以像人類一樣進行數學推理和定理證明。
神經網路可以用來搜尋定理、猜測新定理和尋找反例,如發現了拓樸學中關於結點和邊的關係的新定理,以及在表示論中發現了關於Kazhdan-Lusztig多項式的新結果,但對於證明深奧複雜的定理還有其限制。
自動定理證明系統(ATP)可以自動證明一些複雜的定理,如羅賓斯猜想。但ATP生成的證明往往過於冗長,難以被人類理解。
互動式定理證明系統( ITP)可以用來驗證定理的正確性,幫助發現和修正數學文獻中的錯誤,如數學家Peter Scholze在液體張量實驗(Liquid Tensor Experiment)中承認自己無法掌握所有涉及的數學對象和概念,最終在Lean系統幫助下完成。
大模型如ChatGPT雖然可以產生相關數學內容,但容易產生錯誤。 Buzzard建議大模型與ITP等系統結合使用,透過大模型產生初步證明,然後由ITP進行驗證,從而提高可靠性。
Buzzard認為,這些新興技術可以幫助數學家突破認知障礙,探索更複雜、更新穎的數學領域,並最終改變數學家的工作方式,使他們能夠將更多時間和精力投入到數學思維和理解上。
另外三篇文章,從不同角度探討了這些新興技術如何幫助數學家應對日益增長的複雜性,並開拓新的數學領域。
數學的形式化轉向

邏輯學家Jeremy Avigad討論了自20世紀初以來,數學定義和證明可以在具有精確語法和使用規則的形式系統中表示。
Jeremy Avigad任卡內基美隆大學哲學和數學教授,在數理邏輯和基礎、形式驗證和互動式定理證明以及數學哲學和歷史領域做出了貢獻。

他認為這種轉向可能改變數學的本質,依賴機器驗證的證明可能減少了數學家對直觀理解和洞察的重視,從而可能影響數學發現的過程和數學思想的發展。
純數學中的抽象邊界與規範驅動開發

數學家Johan Commelin和Adam Topaz探討了抽象邊界(Abstraction Boundaries)如何在互動式定理證明器的幫助下,幫助控制數學研究中的複雜性。
Johan Commelin任荷蘭烏特勒支大學助理教授,Adam Topaz阿爾伯塔大學助理教授,兩人研究興趣的交點是代數幾何,共同參與了液體張量試驗。

△左:Johan Commelin,右:Adam Topaz
抽象邊界是指在數學研究和定理證明過程中,將數學物件的實作細節與其外在屬性和行為進行形式區分的界限。這種界限使得數學家可以在不依賴具體實現細節的情況下,使用和推理這些數學對象。
抽象邊界的概念在軟體工程中非常常見,例如透過C語言的頭檔、物件導向程式設計中的公共方法或函數式程式設計中的typeclass來實作。
基於抽象邊界的「規範驅動開發」方法,不僅降低了認知負荷,還促進了數學家之間的合作,使得工作可以輕鬆分配給具有不同專長的合作者。
奇異新世界:定理證明助手與合成基礎

數學家Michael Shulman認為,現有的電腦程式如Lean證明助手,能夠驗證數學證明的正確性,但它們專門的證明語言對許多數學家來說是一道門檻。
Michael Shulman任聖地牙哥大學副教授,研究領域為範疇論與代數拓樸。

現有的電腦證明助手能夠驗證數學證明的正確性,但它們專門的證明語言對許多數學家來說是一道門檻。大模型有潛力降低這個門檻,使數學家能夠以更熟悉的語言與證明助手互動。
這可能允許數學家使用由模型支持的證明助手探索根本上全新的數學領域,現有的證明助手已經在同倫類型論(homotopy type theory)等領域發揮了這一作用。
目前的人工智慧可以做嚴肅的數學嗎?

紐約大學電腦科學家Ernest Davis指出,目前AI在解決文字描述的數學問題上,無法可靠地結合基礎數學和常識推理。

AI透過三種主要方法嘗試解決數學問題,但每種方法都有其優點和限制。
- 直接產生答案,適用於簡單數學問題。
- 產生可執行程式碼,已在實踐中取得成功。
- 翻譯成邏輯規範,對於複雜問題仍有挑戰。
他认为AI在解决数学奥林匹克问题时可能会依赖于训练数据中的模式,而不是真正理解问题的本质,这与人类通过直观和逻辑推理解决问题的方式有显著差异。
AI真正解決數學問題需要三類知識:基礎數學、語言理解和世界常識。例如理解硬幣的價值和物理特性。常識在解決問題時經常被忽視,但實際上是至關重要的。
基準測試集是評估AI系統效能的重要工具,但它們可能無法全面涵蓋AI的所有能力。
但同時他也指出,儘管AI在處理基礎問題時有限制,但這可能不會影響其進行高階數學研究的能力。
一方面,高階數學研究可能不需要與解決基礎問題相同的常識推理能力。
另一方面,在棋類遊戲上,即使AI無法理解棋局的基本概念,在棋局分析和策略制定上的能力能遠遠超越人類棋手。
數學家如何看待AI?
關於自動化與數學研究的一些想法

菲爾茲獎得主Akshay Venkatesh探討了數學自動化對數學研究的影響。他指出,機器可能大大增強數學解決問題的能力,但也會徹底改變數學的核心問題和價值觀,使其難以被人類所認知。

他分析了當前數學界決定「什麼是重要」的機制,如期刊、獎項、數學理論在應用領域得到認可、教育體系、聘用和資助過程等,都不足以解釋數學界相對較高的共識水平。
他認為「證明」這種特殊的學術交流方式能引發一致同意,類似自由市場中訊息傳播的機制。
AI會導致當前數學界對「重要性」的判斷發生劇變。
機器如何使數學更包容

數學家鄭樂雋(Eugenia Cheng)認為,科技已經在改變人們研究數學的方式,可以利用這些技術讓數學更加包容,而不是讓數學家變得多餘。
鄭樂雋在謝菲爾德大學任教,除了範疇論研究和本科教學之外,她的目標是消除世界上的「數學恐懼症」。

她分析了科技如何影響數學教學、提出問題、協作、傳播以及研究:
- 教學:標準的「粉筆和黑板」式講授變得沒有必要,她開始採用互動性更強的教學方式。同時對學生來說,記憶現在已經無關緊要,應當將大腦留給更有趣的事情
- 提出問題:技術使得任何人都可以在網路上提問並獲得答复,但繼承和放大了數學界的精英主義和競爭性。
- 協作:科技大大便利了遠端協作,使地理位置不再是障礙。電子白板等工具也大大增強了協作的便利性。
- 傳播:網路使論文傳播普及,不再侷限於有限的紙本期刊。這讓論文發表過程更加公開透明,論文品質而非發表管道成為關鍵。
- 研究:透過智慧型手機隨時隨地展開研究,不受地點限制。搜尋引擎等也讓她不必記住所有事實,可以隨時查閱。
總的來說,鄭樂雋認為科技可以讓數學變得更包容,只要數學家善用這些技術,而不是固步自封。
同時她也提出,如果最終機器能做得比人類更好,那很好,她將樂意退出數學領域去彈鋼琴。
機器時代下的證明

數論學家Andrew Granville關注證明的本質以及電腦證明與人類證明之間的關係。

他認為,純數學中的「客觀性」並非如我們所想那樣牢不可破。
- 定義和概念的困難:現代數學中許多概念沒有單一明確的定義,有許多可能的定義和詮釋。這就難以談「客觀」。
- 公理系統的限制:根據哥德爾不完備定理,即使採用一致的公理系統,也無法證明所有關於整數的正確語句。這說明「客觀的」數學基礎是有限制的。
- 歷史演進的影響:不同時代數學家對「數學證明」的理解和標準有所不同,這反映了客觀性標準的變化。
他探討了電腦自動證明可能同時帶來的挑戰和機會。電腦證明可以幫助確認人類直觀證明的正確性,提高可信度。但電腦證明可能取代人類,成為「黑箱」證明。但這種證明可能缺乏人類應有的可理解性和適應性。
Granville希望未來的電腦證明能夠吸收人類證明的優點,在形式化的基礎上保持足夠的靈活性和易理解性。
自動化迫使數學家反思自己的價值觀

哥倫比亞大學數學家Michael Harris強調數學需要吸收其他學科、尤其是人文社科的經驗。

他建議經常反思學科的價值追求和物質基礎,有助於數學家在面對自動化等挑戰時,更好地捍衛數學的核心價值。
此外,他也警示數學界不應被科技公司主導的議程所綁架,科技公司的價值取向與數學家的價值取向並不完全一致,數學家應保持獨立思考的勇氣,而不是被動接受來自產業的價值導向。
更多精彩內容7月發布
特刊的第二部分將於2024年7月發布,內容將包括:
- 自動化與哲學:
形式化所引發的許多問題並不新鮮。 McLarty的文章描述,龐加萊在一個多世紀前就在討論「推理機器」。龐加萊已經關注到形式化證明與數學實踐之間的關係,這一主題在de Toffolli的文章中得到了進一步的探討。
- 科技改變思維
DeDeo的文章檢驗了自動證明對數學家認知過程的潛在影響。
- 深度學習與數學的互動
Bengio和Malkin的文章考慮了進行數學研究對機器學習帶來的特定挑戰。 Fraser和Poggio的文章則提出了與深度學習數學基礎相關的問題。
