• News
  • CUDA's universal matrix multiplication: from entry to proficiency!

CUDA's universal matrix multiplication: from entry to proficiency!


General Matrix Multiplication (GEMM) is a core part of various models and calculations, and is also a standard technique for evaluating computing hardware performance (FLOPS). This article will try to understand high-performance computing and software and hardware systems through the implementation and optimization of GEMM.

1. Basic characteristics of GEMM

1.1 GEMM calculation process and complexity

GEMM is defined as:

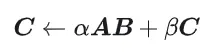
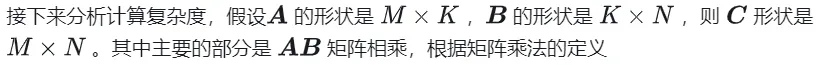
picturepicture

picturepicture

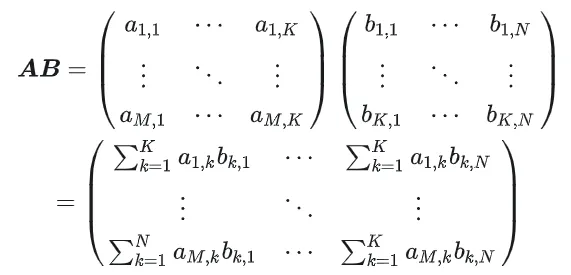
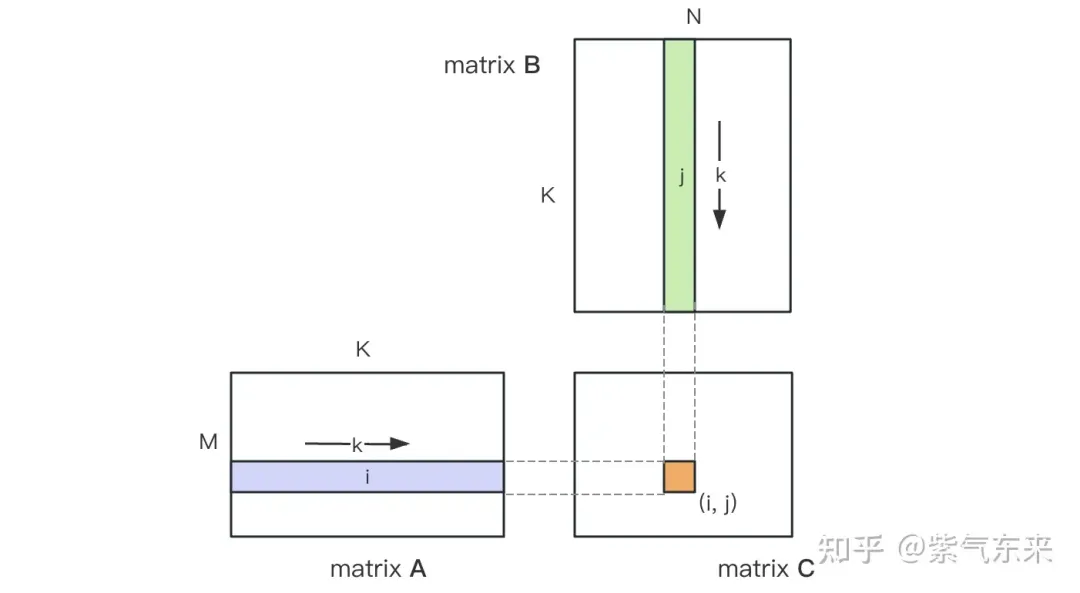
Calculation diagram of matrix multiplication

1.2 Simple implementation and process analysis

picture

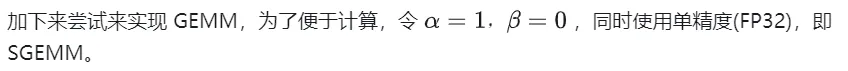
The following is the code implemented on the CPU according to the original definition, which will be used later as a comparison of accuracy.

#define OFFSET(row, col, ld) ((row) * (ld) + (col))

void cpuSgemm(
    float *a, float *b, float *c, const int M, const int N, const int K) {

    for (int m = 0; m < M; m++) {
        for (int n = 0; n < N; n++) {
            float psum = 0.0;
            for (int k = 0; k < K; k++) {
                psum += a[OFFSET(m, k, K)] * b[OFFSET(k, n, N)];
            }
            c[OFFSET(m, n, N)] = psum;
        }
    }
}
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.
  • 15.

Next, CUDA is used to implement Kernal, the simplest matrix multiplication. A total of M * N threads are used to complete the entire matrix multiplication. Each thread is responsible for the calculation of an element in matrix C and needs to complete K times of multiplication and accumulation. Matrices A, B, and C are all stored in global memory ( determined by modifiers). For the complete code, see sgemm_naive.cu. __global__ 

__global__ void naiveSgemm(
    float * __restrict__ a, float * __restrict__ b, float * __restrict__ c,
    const int M, const int N, const int K) {

    int n = blockIdx.x * blockDim.x + threadIdx.x;
    int m = blockIdx.y * blockDim.y + threadIdx.y;
    if (m < M && n < N) {
        float psum = 0.0;
        #pragma unroll
        for (int k = 0; k < K; k++) {
            psum += a[OFFSET(m, k, K)] * b[OFFSET(k, n, N)];
        }
        c[OFFSET(m, n, N)] = psum;
    }
}

const int BM = 32, BN = 32;
const int M = 512, N = 512, K = 512;
dim3 blockDim(BN, BM);
dim3 gridDim((N + BN - 1) / BN, (M + BM - 1) / BM);
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.
  • 15.
  • 16.
  • 17.
  • 18.
  • 19.
  • 20.

The compilation is completed and the results of execution on Tesla V100-PCIE-32GB are as follows. According to the V100 white paper, the peak computing power of FP32 is 15.7 TFLOPS, so the computing power utilization of this method is only 11.5%.

M N K =    128    128   1024, Time =   0.00010083   0.00010260   0.00010874 s, AVG Performance =   304.5951 Gflops
M N K =    192    192   1024, Time =   0.00010173   0.00010198   0.00010253 s, AVG Performance =   689.4680 Gflops
M N K =    256    256   1024, Time =   0.00010266   0.00010318   0.00010384 s, AVG Performance =  1211.4281 Gflops
M N K =    384    384   1024, Time =   0.00019475   0.00019535   0.00019594 s, AVG Performance =  1439.7206 Gflops
M N K =    512    512   1024, Time =   0.00037693   0.00037794   0.00037850 s, AVG Performance =  1322.9753 Gflops
M N K =    768    768   1024, Time =   0.00075238   0.00075558   0.00075776 s, AVG Performance =  1488.9271 Gflops
M N K =   1024   1024   1024, Time =   0.00121562   0.00121669   0.00121789 s, AVG Performance =  1643.8068 Gflops
M N K =   1536   1536   1024, Time =   0.00273072   0.00275611   0.00280208 s, AVG Performance =  1632.7386 Gflops
M N K =   2048   2048   1024, Time =   0.00487622   0.00488028   0.00488614 s, AVG Performance =  1639.2518 Gflops
M N K =   3072   3072   1024, Time =   0.01001603   0.01071136   0.01099990 s, AVG Performance =  1680.4589 Gflops
M N K =   4096   4096   1024, Time =   0.01771046   0.01792170   0.01803462 s, AVG Performance =  1785.5450 Gflops
M N K =   6144   6144   1024, Time =   0.03988969   0.03993405   0.04000595 s, AVG Performance =  1802.9724 Gflops
M N K =   8192   8192   1024, Time =   0.07119219   0.07139694   0.07160816 s, AVG Performance =  1792.7940 Gflops
M N K =  12288  12288   1024, Time =   0.15978026   0.15993242   0.16043369 s, AVG Performance =  1800.7606 Gflops
M N K =  16384  16384   1024, Time =   0.28559187   0.28567238   0.28573316 s, AVG Performance =  1792.2629 Gflops
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.
  • 15.

Let's take M=512, K=512, N=512 as an example to analyze the workflow of the above calculation process in detail:

  1. Allocate storage space for matrices A, B, and C respectively in Global Memory.
  2. Since the calculation of each element in matrix C is independent of each other, each thread in the parallelism mapping corresponds to the calculation of 1 element in matrix C.
  3. Both gridSize and blockSize in execution configuration have two dimensions: x (column direction) and y (row direction), where

picturepicturepicturepicture

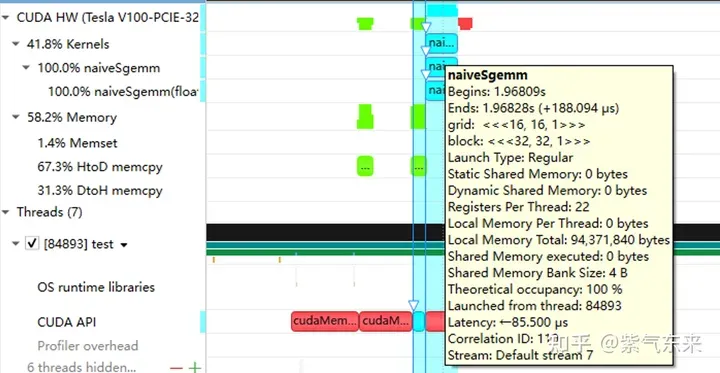
Profiling of the naive version recorded by nsys

2. Research on optimization of GEMM

The previous article only implemented GEMM functionally, and the performance was far from expected. This section will mainly study the optimization of GEMM performance.

2.1 Matrix partitioning using Shared Memory

The above calculation requires two Global Memory loads to complete a multiplication and accumulation operation. The calculation memory access ratio is extremely low, and there is no effective data reuse. Therefore, Shared Memory can be used to reduce repeated memory reads.

First, the matrix C is equally divided into blocks of BMxBN size. Each block is calculated by a Block, and each Thread is responsible for calculating the TMxTN elements in the matrix C. Afterwards, all the data required for calculation is read from smem, which eliminates part of the repeated A and B matrix memory reading. Considering that Shared Memory has limited capacity, BK-sized blocks can be read in K dimensions each time. Such a loop requires a total of K/BK times to complete the entire matrix multiplication operation to obtain the result of the Block. The process is shown in the figure below:

picture

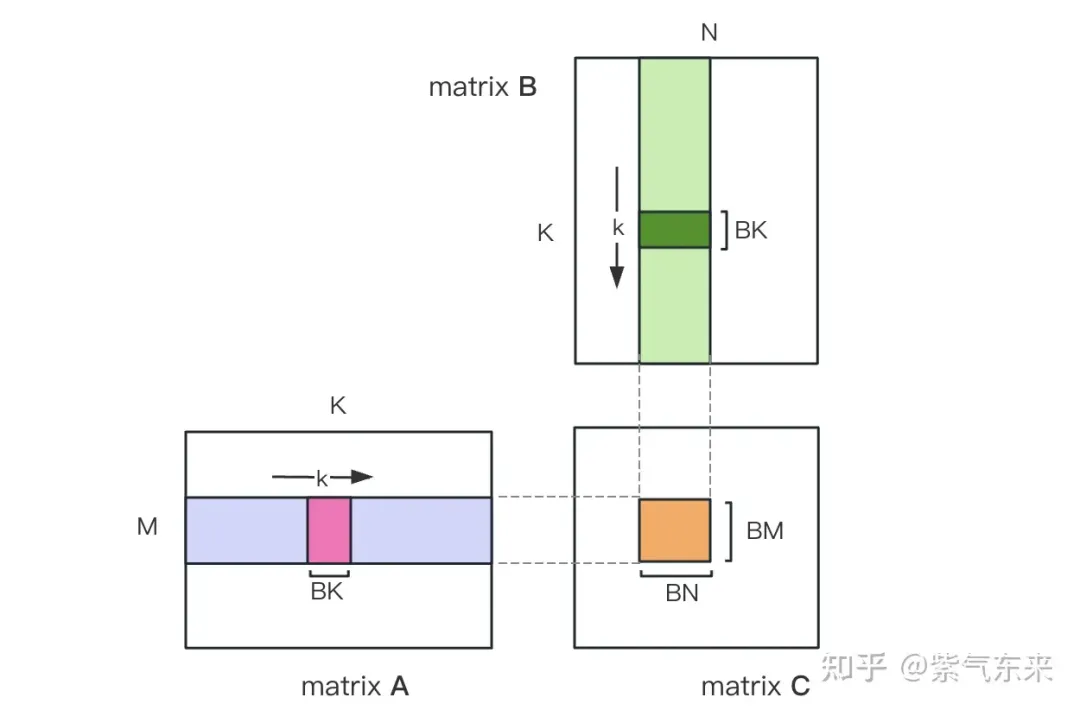
After using Shared Memory optimization, for each block, we can get:

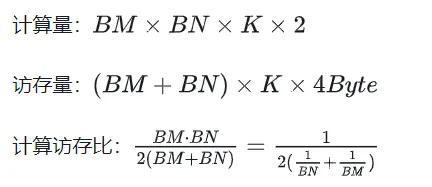
It can be seen from the above formula that the larger the BM and BN are, the higher the calculation memory access ratio will be and the better the performance will be. However, due to the limitation of Shared Memory capacity (V100 1 SM is only 96KB), a Block needs to occupy BK * (BM + BN) * 4 Bytes size.

The values ​​​​of TM and TN are also limited by two aspects. On the one hand, there are limitations on the number of threads. There are BM / TM * BN / TN threads in a block. This number cannot exceed 1024, and cannot be too high to prevent affecting the inter-block space in SM. Parallelism; on the other hand, there is a limit on the number of registers. A thread requires at least TM * TN registers to store the partial sum of matrix C, plus some other registers. The number of all registers cannot exceed 256, and cannot be too high. Prevent affecting the number of parallel threads in SM at the same time.

Finally, BM = BN = 128, BK = 8, TM = TN = 8 are selected, then the calculated memory access ratio is 32. According to the theoretical computing power of V100 15.7TFLOPS, we can get 15.7TFLOPS/32 = 490GB/s. According to the measured HBM bandwidth is 763GB/s, it can be seen that the bandwidth will no longer limit the computing performance at this time.

Based on the above analysis, the kernel function implementation process is as follows. For the complete code, see sgemm_v1.cu. The main steps include:

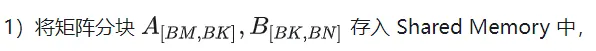
picturepicture

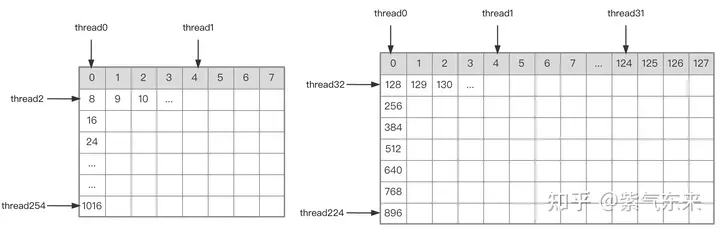
Thread index relationship of AB matrix partitioning

After determining the execution process of a single block, it is necessary to determine the corresponding relationship between the different blocks processed by the multi-block in the Global Memory. A is still used as an example for explanation. Since the block moves along the direction of the row, you first need to determine the row number. According to the two-dimensional global linear index relationship of the Grid, by * BM it represents the starting row number of load_a_smem_m the block. At the same time, we know the row number inside the block, so The global line number is load_a_gmem_m = by * BM + load_a_smem_m . Since the chunks move along the direction of the row, the columns change and need to be calculated inside the loop. The starting column number is also calculated first to bk * BK speed up the internal column number load_a_smem_k of the chunk. From this, we can determine the location of the chunk in the original data. Position in OFFSET( , K) . In the same way, the matrix partitioning situation can be analyzed and will not be repeated. load_a_gmem_k = bk * BK + load_a_smem_k load_a_gmem_m, load_a_gmem_k

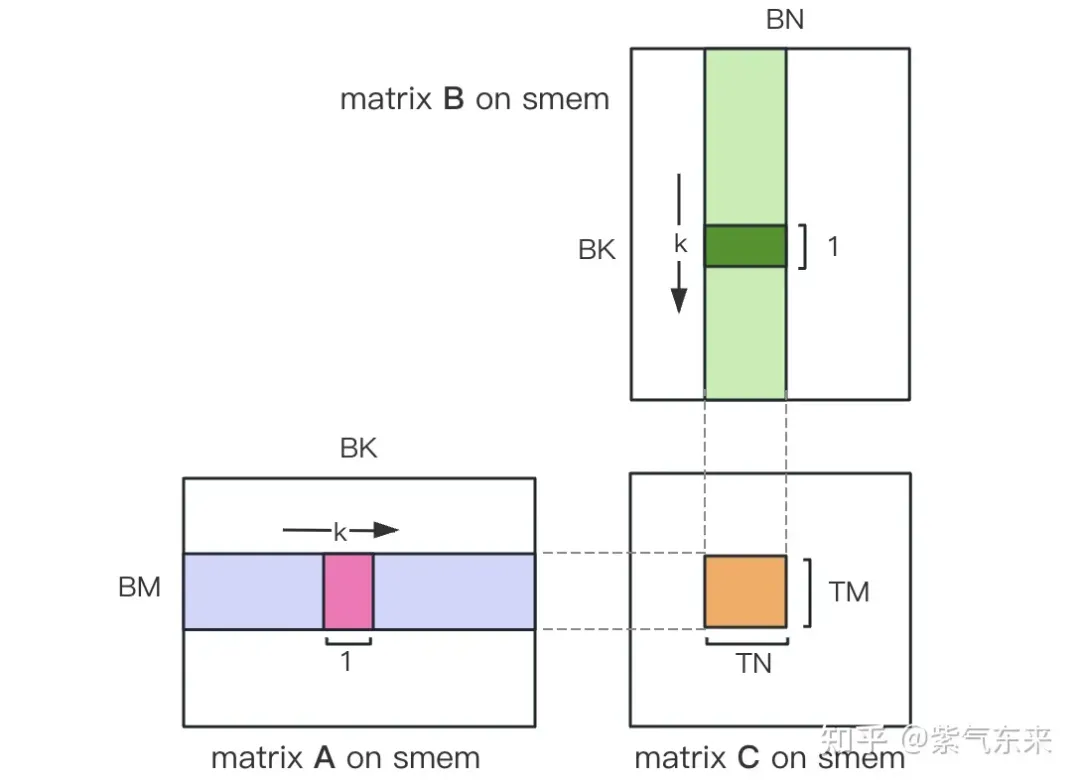
picturepicture

After the calculation is completed, it needs to be stored in Global Memory, which requires calculating its corresponding relationship in Global Memory. Due to the existence of smaller blocks, both rows and columns are composed of 3 parts: the global row number store_c_gmem_m is equal to the starting row number of the large block by * BM+ the starting row number of the small block ty * TM+ the relative row number within the small block . The same goes for columns. i 

__global__ void sgemm_V1(
    float * __restrict__ a, float * __restrict__ b, float * __restrict__ c,
    const int M, const int N, const int K) {

    const int BM = 128;
    const int BN = 128;
    const int BK = 8;
    const int TM = 8;
    const int TN = 8;

    const int bx = blockIdx.x;
    const int by = blockIdx.y;
    const int tx = threadIdx.x;
    const int ty = threadIdx.y;
    const int tid = ty * blockDim.x + tx;

    __shared__ float s_a[BM][BK];
    __shared__ float s_b[BK][BN];

    float r_c[TM][TN] = {0.0};

    int load_a_smem_m = tid >> 1;  // tid/2, row of s_a
    int load_a_smem_k = (tid & 1) << 2;  // (tid % 2 == 0) ? 0 : 4, col of s_a
    int load_b_smem_k = tid >> 5;   // tid/32, row of s_b
    int load_b_smem_n = (tid & 31) << 2;  // (tid % 32) * 4, col of s_b

    int load_a_gmem_m = by * BM + load_a_smem_m;  // global row of a
    int load_b_gmem_n = bx * BN + load_b_smem_n;  // global col of b

    for (int bk = 0; bk < (K + BK - 1) / BK; bk++) {
        int load_a_gmem_k = bk * BK + load_a_smem_k;   // global col of a
        int load_a_gmem_addr = OFFSET(load_a_gmem_m, load_a_gmem_k, K);
        FLOAT4(s_a[load_a_smem_m][load_a_smem_k]) = FLOAT4(a[load_a_gmem_addr]);
        int load_b_gmem_k = bk * BK + load_b_smem_k;   // global row of b
        int load_b_gmem_addr = OFFSET(load_b_gmem_k, load_b_gmem_n, N);
        FLOAT4(s_b[load_b_smem_k][load_b_smem_n]) = FLOAT4(b[load_b_gmem_addr]);
        __syncthreads();

        #pragma unroll
        for (int k = 0; k < BK; k++) {
            #pragma unroll
            for (int m = 0; m < TM; m++) {
                #pragma unroll
                for (int n = 0; n < TN; n++) {
                    int comp_a_smem_m = ty * TM + m;
                    int comp_b_smem_n = tx * TN + n;
                    r_c[m][n] += s_a[comp_a_smem_m][k] * s_b[k][comp_b_smem_n];
                }
            }
        }

        __syncthreads();
    }

    #pragma unroll
    for (int i = 0; i < TM; i++) {
        int store_c_gmem_m = by * BM + ty * TM + i;
        #pragma unroll
        for (int j = 0; j < TN; j += 4) {
            int store_c_gmem_n = bx * BN + tx * TN + j;
            int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);
            FLOAT4(c[store_c_gmem_addr]) = FLOAT4(r_c[i][j]);
        }
    }
}
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.
  • 15.
  • 16.
  • 17.
  • 18.
  • 19.
  • 20.
  • twenty one.
  • twenty two.
  • twenty three.
  • twenty four.
  • 25.
  • 26.
  • 27.
  • 28.
  • 29.
  • 30.
  • 31.
  • 32.
  • 33.
  • 34.
  • 35.
  • 36.
  • 37.
  • 38.
  • 39.
  • 40.
  • 41.
  • 42.
  • 43.
  • 44.
  • 45.
  • 46.
  • 47.
  • 48.
  • 49.
  • 50.
  • 51.
  • 52.
  • 53.
  • 54.
  • 55.
  • 56.
  • 57.
  • 58.
  • 59.
  • 60.
  • 61.
  • 62.
  • 63.
  • 64.
  • 65.

计算结果如下，性能达到了理论峰值性能的51.7%：

M N K =    128    128   1024, Time =   0.00031578   0.00031727   0.00032288 s, AVG Performance =    98.4974 Gflops
M N K =    192    192   1024, Time =   0.00031638   0.00031720   0.00031754 s, AVG Performance =   221.6661 Gflops
M N K =    256    256   1024, Time =   0.00031488   0.00031532   0.00031606 s, AVG Performance =   396.4287 Gflops
M N K =    384    384   1024, Time =   0.00031686   0.00031814   0.00032080 s, AVG Performance =   884.0425 Gflops
M N K =    512    512   1024, Time =   0.00031814   0.00032007   0.00032493 s, AVG Performance =  1562.1563 Gflops
M N K =    768    768   1024, Time =   0.00032397   0.00034419   0.00034848 s, AVG Performance =  3268.5245 Gflops
M N K =   1024   1024   1024, Time =   0.00034570   0.00034792   0.00035331 s, AVG Performance =  5748.3952 Gflops
M N K =   1536   1536   1024, Time =   0.00068797   0.00068983   0.00069094 s, AVG Performance =  6523.3424 Gflops
M N K =   2048   2048   1024, Time =   0.00136173   0.00136552   0.00136899 s, AVG Performance =  5858.5604 Gflops
M N K =   3072   3072   1024, Time =   0.00271910   0.00273115   0.00274006 s, AVG Performance =  6590.6331 Gflops
M N K =   4096   4096   1024, Time =   0.00443805   0.00445964   0.00446883 s, AVG Performance =  7175.4698 Gflops
M N K =   6144   6144   1024, Time =   0.00917891   0.00950608   0.00996963 s, AVG Performance =  7574.0999 Gflops
M N K =   8192   8192   1024, Time =   0.01628838   0.01645271   0.01660790 s, AVG Performance =  7779.8733 Gflops
M N K =  12288  12288   1024, Time =   0.03592557   0.03597434   0.03614323 s, AVG Performance =  8005.7066 Gflops
M N K =  16384  16384   1024, Time =   0.06304122   0.06306373   0.06309302 s, AVG Performance =  8118.7715 Gflops
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.
  • 15.

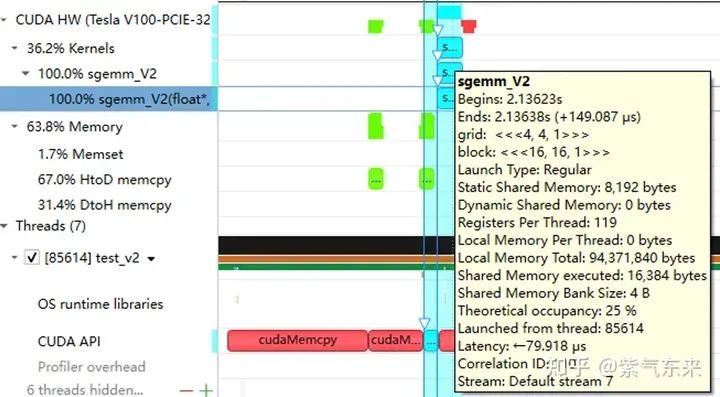
下面仍以M=512,K=512,N=512为例，分析一下结果。首先通过 profiling 可以看到 Shared Memory 占用为 8192 bytes，这与理论上(128+128)X8X4完全一致。

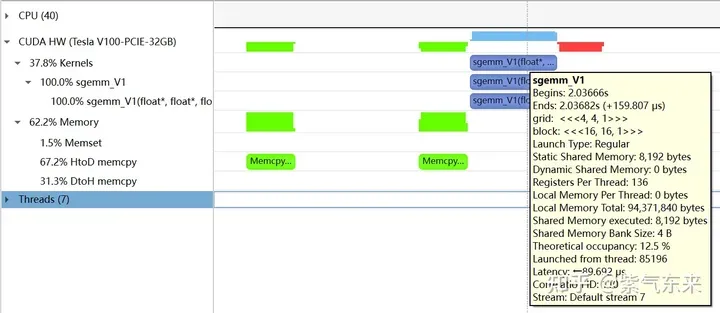picturensys 记录 的 V1 版本的 profiling

profiling 显示 Occupancy 为 12.5%，可以通过 cuda-calculator 加以印证，该例中 threads per block = 256, Registers per thread = 136, 由此可以计算得到每个SM中活跃的 warp 为8，而对于V100，每个SM中的 warp 总数为64，因此 Occupancy 为 8/64 = 12.5%。

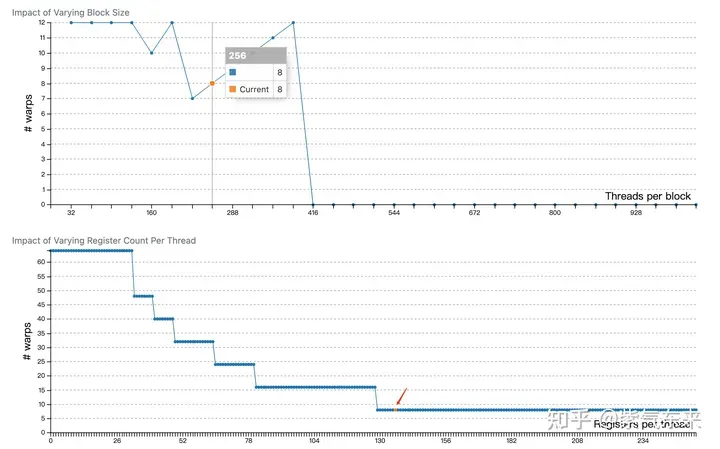
2.2 解决 Bank Conflict 问题

上节通过利用 Shared Memory 大幅提高了访存效率，进而提高了性能，本节将进一步优化 Shared Memory 的使用。

Shared Memory一共划分为32个Bank，每个Bank的宽度为4 Bytes，如果需要访问同一个Bank的多个数据，就会发生Bank Conflict。例如一个Warp的32个线程，如果访问的地址分别为0、4、8、...、124，就不会发生Bank Conflict，只占用Shared Memory一拍的时间；如果访问的地址为0、8、16、...、248，这样一来地址0和地址128对应的数据位于同一Bank、地址4和地址132对应的数据位于同一Bank，以此类推，那么就需要占用Shared Memory两拍的时间才能读出。

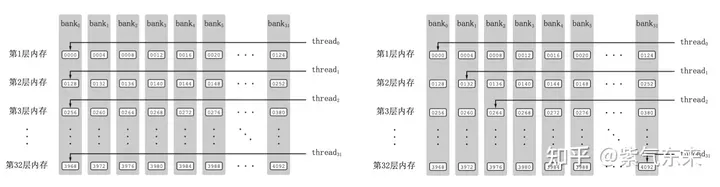
有 Bank Conflict VS 无 Bank Conflict

再看 V1 版本计算部分的三层循环，每次从Shared memory中取矩阵A的长度为TM的向量和矩阵B的长度为TN的向量，这两个向量做外积并累加到部分和中，一次外积共TM * TN次乘累加，一共需要循环BK次取数和外积。

接下来分析从Shared Memory load的过程中存在的Bank Conflict：

i) 取矩阵A需要取一个列向量，而矩阵A在Shared Memory中是按行存储的；

ii) 在TM = TN = 8的情况下，无论矩阵A还是矩阵B，从Shared Memory中取数时需要取连续的8个数，即便用LDS.128指令一条指令取四个数，也需要两条指令，由于一个线程的两条load指令的地址是连续的，那么同一个Warp不同线程的同一条load指令的访存地址就是被间隔开的，便存在着 Bank Conflict。

为了解决上述的两点Shared Memory的Bank Conflict，采用了一下两点优化：

i) 为矩阵A分配Shared Memory时形状分配为[BK][BM]，即让矩阵A在Shared Memory中按列存储

ii) 将原本每个线程负责计算的TM * TN的矩阵C，划分为下图中这样的两块TM/2 * TN的矩阵C，由于TM/2=4，一条指令即可完成A的一块的load操作，两个load可同时进行。

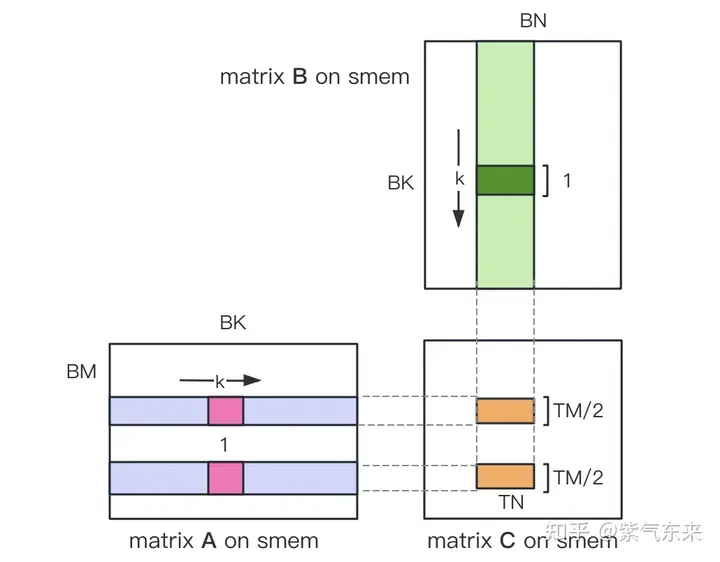
kernel 函数的核心部分实现如下，完整代码见 sgemm_v2.cu 。

__shared__ float s_a[BK][BM];
    __shared__ float s_b[BK][BN];

    float r_load_a[4];
    float r_load_b[4];
    float r_comp_a[TM];
    float r_comp_b[TN];
    float r_c[TM][TN] = {0.0};

    int load_a_smem_m = tid >> 1;
    int load_a_smem_k = (tid & 1) << 2;
    int load_b_smem_k = tid >> 5;
    int load_b_smem_n = (tid & 31) << 2;

    int load_a_gmem_m = by * BM + load_a_smem_m;
    int load_b_gmem_n = bx * BN + load_b_smem_n;

    for (int bk = 0; bk < (K + BK - 1) / BK; bk++) {

        int load_a_gmem_k = bk * BK + load_a_smem_k;
        int load_a_gmem_addr = OFFSET(load_a_gmem_m, load_a_gmem_k, K);
        int load_b_gmem_k = bk * BK + load_b_smem_k;
        int load_b_gmem_addr = OFFSET(load_b_gmem_k, load_b_gmem_n, N);
        FLOAT4(r_load_a[0]) = FLOAT4(a[load_a_gmem_addr]);
        FLOAT4(r_load_b[0]) = FLOAT4(b[load_b_gmem_addr]);

        s_a[load_a_smem_k    ][load_a_smem_m] = r_load_a[0];
        s_a[load_a_smem_k + 1][load_a_smem_m] = r_load_a[1];
        s_a[load_a_smem_k + 2][load_a_smem_m] = r_load_a[2];
        s_a[load_a_smem_k + 3][load_a_smem_m] = r_load_a[3];
        FLOAT4(s_b[load_b_smem_k][load_b_smem_n]) = FLOAT4(r_load_b[0]);

        __syncthreads();

        #pragma unroll
        for (int tk = 0; tk < BK; tk++) {
            FLOAT4(r_comp_a[0]) = FLOAT4(s_a[tk][ty * TM / 2         ]);
            FLOAT4(r_comp_a[4]) = FLOAT4(s_a[tk][ty * TM / 2 + BM / 2]);
            FLOAT4(r_comp_b[0]) = FLOAT4(s_b[tk][tx * TN / 2         ]);
            FLOAT4(r_comp_b[4]) = FLOAT4(s_b[tk][tx * TN / 2 + BN / 2]);

            #pragma unroll
            for (int tm = 0; tm < TM; tm++) {
                #pragma unroll
                for (int tn = 0; tn < TN; tn++) {
                    r_c[tm][tn] += r_comp_a[tm] * r_comp_b[tn];
                }
            }
        }

        __syncthreads();
    }

    #pragma unroll
    for (int i = 0; i < TM / 2; i++) {
        int store_c_gmem_m = by * BM + ty * TM / 2 + i;
        int store_c_gmem_n = bx * BN + tx * TN / 2;
        int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);
        FLOAT4(c[store_c_gmem_addr]) = FLOAT4(r_c[i][0]);
        FLOAT4(c[store_c_gmem_addr + BN / 2]) = FLOAT4(r_c[i][4]);
    }
    #pragma unroll
    for (int i = 0; i < TM / 2; i++) {
        int store_c_gmem_m = by * BM + BM / 2 + ty * TM / 2 + i;
        int store_c_gmem_n = bx * BN + tx * TN / 2;
        int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);
        FLOAT4(c[store_c_gmem_addr]) = FLOAT4(r_c[i + TM / 2][0]);
        FLOAT4(c[store_c_gmem_addr + BN / 2]) = FLOAT4(r_c[i + TM / 2][4]);
    }
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.
  • 15.
  • 16.
  • 17.
  • 18.
  • 19.
  • 20.
  • 21.
  • 22.
  • 23.
  • 24.
  • 25.
  • 26.
  • 27.
  • 28.
  • 29.
  • 30.
  • 31.
  • 32.
  • 33.
  • 34.
  • 35.
  • 36.
  • 37.
  • 38.
  • 39.
  • 40.
  • 41.
  • 42.
  • 43.
  • 44.
  • 45.
  • 46.
  • 47.
  • 48.
  • 49.
  • 50.
  • 51.
  • 52.
  • 53.
  • 54.
  • 55.
  • 56.
  • 57.
  • 58.
  • 59.
  • 60.
  • 61.
  • 62.
  • 63.
  • 64.
  • 65.
  • 66.
  • 67.
  • 68.
  • 69.

结果如下，相对未解决 Bank Conflict 版(V1) 性能提高了 14.4%，达到了理论峰值的74.3%。

M N K =    128    128   1024, Time =   0.00029699   0.00029918   0.00030989 s, AVG Performance =   104.4530 Gflops
M N K =    192    192   1024, Time =   0.00029776   0.00029828   0.00029882 s, AVG Performance =   235.7252 Gflops
M N K =    256    256   1024, Time =   0.00029485   0.00029530   0.00029619 s, AVG Performance =   423.2949 Gflops
M N K =    384    384   1024, Time =   0.00029734   0.00029848   0.00030090 s, AVG Performance =   942.2843 Gflops
M N K =    512    512   1024, Time =   0.00029853   0.00029945   0.00030070 s, AVG Performance =  1669.7479 Gflops
M N K =    768    768   1024, Time =   0.00030458   0.00032467   0.00032790 s, AVG Performance =  3465.1038 Gflops
M N K =   1024   1024   1024, Time =   0.00032406   0.00032494   0.00032621 s, AVG Performance =  6155.0281 Gflops
M N K =   1536   1536   1024, Time =   0.00047990   0.00048224   0.00048461 s, AVG Performance =  9331.3912 Gflops
M N K =   2048   2048   1024, Time =   0.00094426   0.00094636   0.00094992 s, AVG Performance =  8453.4569 Gflops
M N K =   3072   3072   1024, Time =   0.00187866   0.00188096   0.00188538 s, AVG Performance =  9569.5816 Gflops
M N K =   4096   4096   1024, Time =   0.00312589   0.00319050   0.00328147 s, AVG Performance = 10029.7885 Gflops
M N K =   6144   6144   1024, Time =   0.00641280   0.00658940   0.00703498 s, AVG Performance = 10926.6372 Gflops
M N K =   8192   8192   1024, Time =   0.01101130   0.01116194   0.01122950 s, AVG Performance = 11467.5446 Gflops
M N K =  12288  12288   1024, Time =   0.02464854   0.02466705   0.02469344 s, AVG Performance = 11675.4946 Gflops
M N K =  16384  16384   1024, Time =   0.04385955   0.04387468   0.04388355 s, AVG Performance = 11669.5995 Gflops
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.
  • 15.

分析一下 profiling 可以看到 Static Shared Memory 仍然是使用了8192 Bytes，奇怪的的是，Shared Memory executed 却翻倍变成了 16384 Bytes（知友如果知道原因可以告诉我一下）。

picture

2.3 流水并行化：Double Buffering

Double Buffering，即双缓冲，即通过增加buffer的方式，使得 访存-计算 的串行模式流水线化，以减少等待时间，提高计算效率，其原理如下图所示:

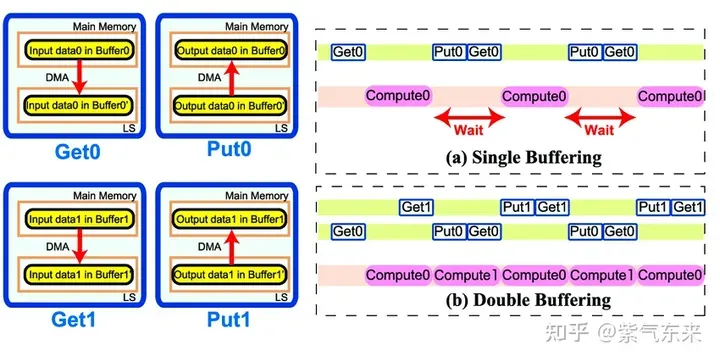
Single Buffering VS Double Buffering

具体到 GEMM 任务中来，就是需要两倍的Shared Memory，之前只需要BK * (BM + BN) * 4 Bytes的Shared Memory，采用Double Buffering之后需要2BK * (BM + BN) * 4 Bytes的Shared Memory，然后使其 pipeline 流动起来。

代码核心部分如下所示，完整代码参见 sgemm_v3.cu 。有以下几点需要注意：

1）主循环从bk = 1 开始，第一次数据加载在主循环之前，最后一次计算在主循环之后，这是pipeline 的特点决定的；

2）由于计算和下一次访存使用的Shared Memory不同，因此主循环中每次循环只需要一次__syncthreads()即可

3）由于GPU不能向CPU那样支持乱序执行，主循环中需要先将下一次循环计算需要的Gloabal Memory中的数据load 到寄存器，然后进行本次计算，之后再将load到寄存器中的数据写到Shared Memory，这样在LDG指令向Global Memory做load时，不会影响后续FFMA及其它运算指令的 launch 执行，也就达到了Double Buffering的目的。

__shared__ float s_a[2][BK][BM];
    __shared__ float s_b[2][BK][BN];

    float r_load_a[4];
    float r_load_b[4];
    float r_comp_a[TM];
    float r_comp_b[TN];
    float r_c[TM][TN] = {0.0};

    int load_a_smem_m = tid >> 1;
    int load_a_smem_k = (tid & 1) << 2;
    int load_b_smem_k = tid >> 5;
    int load_b_smem_n = (tid & 31) << 2;

    int load_a_gmem_m = by * BM + load_a_smem_m;
    int load_b_gmem_n = bx * BN + load_b_smem_n;

    {
        int load_a_gmem_k = load_a_smem_k;
        int load_a_gmem_addr = OFFSET(load_a_gmem_m, load_a_gmem_k, K);
        int load_b_gmem_k = load_b_smem_k;
        int load_b_gmem_addr = OFFSET(load_b_gmem_k, load_b_gmem_n, N);
        FLOAT4(r_load_a[0]) = FLOAT4(a[load_a_gmem_addr]);
        FLOAT4(r_load_b[0]) = FLOAT4(b[load_b_gmem_addr]);

        s_a[0][load_a_smem_k    ][load_a_smem_m] = r_load_a[0];
        s_a[0][load_a_smem_k + 1][load_a_smem_m] = r_load_a[1];
        s_a[0][load_a_smem_k + 2][load_a_smem_m] = r_load_a[2];
        s_a[0][load_a_smem_k + 3][load_a_smem_m] = r_load_a[3];
        FLOAT4(s_b[0][load_b_smem_k][load_b_smem_n]) = FLOAT4(r_load_b[0]);
    }

    for (int bk = 1; bk < (K + BK - 1) / BK; bk++) {

        int smem_sel = (bk - 1) & 1;
        int smem_sel_next = bk & 1;

        int load_a_gmem_k = bk * BK + load_a_smem_k;
        int load_a_gmem_addr = OFFSET(load_a_gmem_m, load_a_gmem_k, K);
        int load_b_gmem_k = bk * BK + load_b_smem_k;
        int load_b_gmem_addr = OFFSET(load_b_gmem_k, load_b_gmem_n, N);
        FLOAT4(r_load_a[0]) = FLOAT4(a[load_a_gmem_addr]);
        FLOAT4(r_load_b[0]) = FLOAT4(b[load_b_gmem_addr]);

        #pragma unroll
        for (int tk = 0; tk < BK; tk++) {
            FLOAT4(r_comp_a[0]) = FLOAT4(s_a[smem_sel][tk][ty * TM / 2         ]);
            FLOAT4(r_comp_a[4]) = FLOAT4(s_a[smem_sel][tk][ty * TM / 2 + BM / 2]);
            FLOAT4(r_comp_b[0]) = FLOAT4(s_b[smem_sel][tk][tx * TN / 2         ]);
            FLOAT4(r_comp_b[4]) = FLOAT4(s_b[smem_sel][tk][tx * TN / 2 + BN / 2]);

            #pragma unroll
            for (int tm = 0; tm < TM; tm++) {
                #pragma unroll
                for (int tn = 0; tn < TN; tn++) {
                    r_c[tm][tn] += r_comp_a[tm] * r_comp_b[tn];
                }
            }
        }

        s_a[smem_sel_next][load_a_smem_k    ][load_a_smem_m] = r_load_a[0];
        s_a[smem_sel_next][load_a_smem_k + 1][load_a_smem_m] = r_load_a[1];
        s_a[smem_sel_next][load_a_smem_k + 2][load_a_smem_m] = r_load_a[2];
        s_a[smem_sel_next][load_a_smem_k + 3][load_a_smem_m] = r_load_a[3];
        FLOAT4(s_b[smem_sel_next][load_b_smem_k][load_b_smem_n]) = FLOAT4(r_load_b[0]);

        __syncthreads();
    }

    #pragma unroll
    for (int tk = 0; tk < BK; tk++) {
        FLOAT4(r_comp_a[0]) = FLOAT4(s_a[1][tk][ty * TM / 2         ]);
        FLOAT4(r_comp_a[4]) = FLOAT4(s_a[1][tk][ty * TM / 2 + BM / 2]);
        FLOAT4(r_comp_b[0]) = FLOAT4(s_b[1][tk][tx * TN / 2         ]);
        FLOAT4(r_comp_b[4]) = FLOAT4(s_b[1][tk][tx * TN / 2 + BN / 2]);

        #pragma unroll
        for (int tm = 0; tm < TM; tm++) {
            #pragma unroll
            for (int tn = 0; tn < TN; tn++) {
                r_c[tm][tn] += r_comp_a[tm] * r_comp_b[tn];
            }
        }
    }

    #pragma unroll
    for (int i = 0; i < TM / 2; i++) {
        int store_c_gmem_m = by * BM + ty * TM / 2 + i;
        int store_c_gmem_n = bx * BN + tx * TN / 2;
        int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);
        FLOAT4(c[store_c_gmem_addr]) = FLOAT4(r_c[i][0]);
        FLOAT4(c[store_c_gmem_addr + BN / 2]) = FLOAT4(r_c[i][4]);
    }
    #pragma unroll
    for (int i = 0; i < TM / 2; i++) {
        int store_c_gmem_m = by * BM + BM / 2 + ty * TM / 2 + i;
        int store_c_gmem_n = bx * BN + tx * TN / 2;
        int store_c_gmem_addr = OFFSET(store_c_gmem_m, store_c_gmem_n, N);
        FLOAT4(c[store_c_gmem_addr]) = FLOAT4(r_c[i + TM / 2][0]);
        FLOAT4(c[store_c_gmem_addr + BN / 2]) = FLOAT4(r_c[i + TM / 2][4]);
    }
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.
  • 15.
  • 16.
  • 17.
  • 18.
  • 19.
  • 20.
  • 21.
  • 22.
  • 23.
  • 24.
  • 25.
  • 26.
  • 27.
  • 28.
  • 29.
  • 30.
  • 31.
  • 32.
  • 33.
  • 34.
  • 35.
  • 36.
  • 37.
  • 38.
  • 39.
  • 40.
  • 41.
  • 42.
  • 43.
  • 44.
  • 45.
  • 46.
  • 47.
  • 48.
  • 49.
  • 50.
  • 51.
  • 52.
  • 53.
  • 54.
  • 55.
  • 56.
  • 57.
  • 58.
  • 59.
  • 60.
  • 61.
  • 62.
  • 63.
  • 64.
  • 65.
  • 66.
  • 67.
  • 68.
  • 69.
  • 70.
  • 71.
  • 72.
  • 73.
  • 74.
  • 75.
  • 76.
  • 77.
  • 78.
  • 79.
  • 80.
  • 81.
  • 82.
  • 83.
  • 84.
  • 85.
  • 86.
  • 87.
  • 88.
  • 89.
  • 90.
  • 91.
  • 92.
  • 93.
  • 94.
  • 95.
  • 96.
  • 97.
  • 98.
  • 99.
  • 100.
  • 101.

性能如下所示，达到了理论峰值的 80.6%。

M N K =    128    128   1024, Time =   0.00024000   0.00024240   0.00025792 s, AVG Performance =   128.9191 Gflops
M N K =    192    192   1024, Time =   0.00024000   0.00024048   0.00024125 s, AVG Performance =   292.3840 Gflops
M N K =    256    256   1024, Time =   0.00024029   0.00024114   0.00024272 s, AVG Performance =   518.3728 Gflops
M N K =    384    384   1024, Time =   0.00024070   0.00024145   0.00024198 s, AVG Performance =  1164.8394 Gflops
M N K =    512    512   1024, Time =   0.00024173   0.00024237   0.00024477 s, AVG Performance =  2062.9786 Gflops
M N K =    768    768   1024, Time =   0.00024291   0.00024540   0.00026010 s, AVG Performance =  4584.3820 Gflops
M N K =   1024   1024   1024, Time =   0.00024534   0.00024631   0.00024941 s, AVG Performance =  8119.7302 Gflops
M N K =   1536   1536   1024, Time =   0.00045712   0.00045780   0.00045872 s, AVG Performance =  9829.5167 Gflops
M N K =   2048   2048   1024, Time =   0.00089632   0.00089970   0.00090656 s, AVG Performance =  8891.8924 Gflops
M N K =   3072   3072   1024, Time =   0.00177891   0.00178289   0.00178592 s, AVG Performance = 10095.9883 Gflops
M N K =   4096   4096   1024, Time =   0.00309763   0.00310057   0.00310451 s, AVG Performance = 10320.6843 Gflops
M N K =   6144   6144   1024, Time =   0.00604826   0.00619887   0.00663078 s, AVG Performance = 11615.0253 Gflops
M N K =   8192   8192   1024, Time =   0.01031738   0.01045051   0.01048861 s, AVG Performance = 12248.2036 Gflops
M N K =  12288  12288   1024, Time =   0.02283978   0.02285837   0.02298272 s, AVG Performance = 12599.3212 Gflops
M N K =  16384  16384   1024, Time =   0.04043287   0.04044823   0.04046151 s, AVG Performance = 12658.1556 Gflops
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.
  • 15.

从 profiling 可以看到双倍的 Shared Memory 的占用

三、cuBLAS 实现方式探究

本节我们将认识CUDA的标准库——cuBLAS， 即NVIDIA版本的基本线性代数子程序 (Basic Linear Algebra Subprograms, BLAS) 规范实现代码。它支持 Level 1 (向量与向量运算) ，Level 2 (向量与矩阵运算) ，Level 3 (矩阵与矩阵运算) 级别的标准矩阵运算。

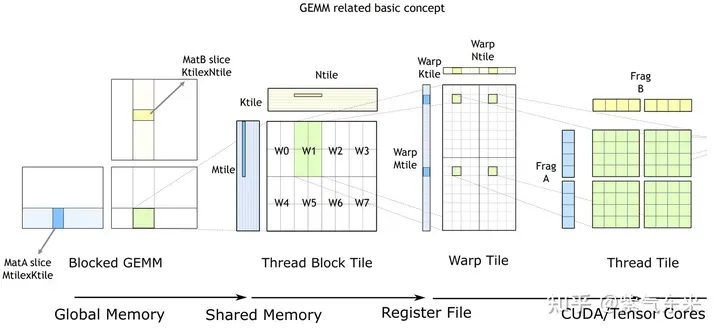
cuBLAS/CUTLASS GEMM的基本过程

As shown in the figure above, the calculation process is decomposed into a hierarchical structure of thread block tiles , warp tiles and thread tiles, and AMP's strategy is applied to this hierarchical structure to complete it efficiently. GPU-based GEMM split into tiles. This hierarchy closely reflects the NVIDIA CUDA programming model. You can see data movement from global memory to shared memory (matrix to thread block tile); data movement from shared memory to registers (thread block tile to warp tile); calculations from registers to CUDA core (warp tile to thread tile) ).

cuBLAS implements the single-precision matrix multiplication function cublasSgemm. Its main parameters are as follows:

cublasStatus_t cublasSgemm( cublasHandle_t handle, // 调用 cuBLAS 库时的句柄 
                            cublasOperation_t transa, // A 矩阵是否需要转置 
                            cublasOperation_t transb, // B 矩阵是否需要转置 
                            int m, // A 的行数 
                            int n, // B 的列数 
                            int k, // A 的列数 
                            const float *alpha, // 系数 α, host or device pointer 
                            const float *A, // 矩阵 A 的指针，device pointer 
                            int lda, // 矩阵 A 的主维，if A 转置， lda = max(1, k), else max(1, m) 
                            const float *B, // 矩阵 B 的指针, device pointer 
                            int ldb, // 矩阵 B 的主维，if B 转置， ldb = max(1, n), else max(1, k) 
                            const float *beta, // 系数 β, host or device pointer 
                            float *C, // 矩阵 C 的指针，device pointer 
                            int ldc // 矩阵 C 的主维，ldc >= max(1, m) );
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.

The calling method is as follows:

cublasHandle_t cublas_handle;
cublasCreate(&cublas_handle);
float cublas_alpha = 1.0;
float cublas_beta = 0;
cublasSgemm(cublas_handle, CUBLAS_OP_N, CUBLAS_OP_N, N, M, K, &cublas_alpha, d_b, N, d_a, K, &cublas_beta, d_c, N);
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.

Performance is shown below, reaching 82.4% of the theoretical peak.

M N K =    128    128   1024, Time =   0.00002704   0.00003634   0.00010822 s, AVG Performance =   860.0286 Gflops
M N K =    192    192   1024, Time =   0.00003155   0.00003773   0.00007267 s, AVG Performance =  1863.6689 Gflops
M N K =    256    256   1024, Time =   0.00003917   0.00004524   0.00007747 s, AVG Performance =  2762.9438 Gflops
M N K =    384    384   1024, Time =   0.00005318   0.00005978   0.00009120 s, AVG Performance =  4705.0655 Gflops
M N K =    512    512   1024, Time =   0.00008326   0.00010280   0.00013840 s, AVG Performance =  4863.9646 Gflops
M N K =    768    768   1024, Time =   0.00014278   0.00014867   0.00018816 s, AVG Performance =  7567.1560 Gflops
M N K =   1024   1024   1024, Time =   0.00023485   0.00024460   0.00028150 s, AVG Performance =  8176.5614 Gflops
M N K =   1536   1536   1024, Time =   0.00046474   0.00047607   0.00051181 s, AVG Performance =  9452.3201 Gflops
M N K =   2048   2048   1024, Time =   0.00077930   0.00087862   0.00092307 s, AVG Performance =  9105.2126 Gflops
M N K =   3072   3072   1024, Time =   0.00167904   0.00168434   0.00171114 s, AVG Performance = 10686.6837 Gflops
M N K =   4096   4096   1024, Time =   0.00289619   0.00291068   0.00295904 s, AVG Performance = 10994.0128 Gflops
M N K =   6144   6144   1024, Time =   0.00591766   0.00594586   0.00596915 s, AVG Performance = 12109.2611 Gflops
M N K =   8192   8192   1024, Time =   0.01002384   0.01017465   0.01028435 s, AVG Performance = 12580.2896 Gflops
M N K =  12288  12288   1024, Time =   0.02231159   0.02233805   0.02245619 s, AVG Performance = 12892.7969 Gflops
M N K =  16384  16384   1024, Time =   0.03954650   0.03959291   0.03967242 s, AVG Performance = 12931.6086 Gflops
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.
  • 15.

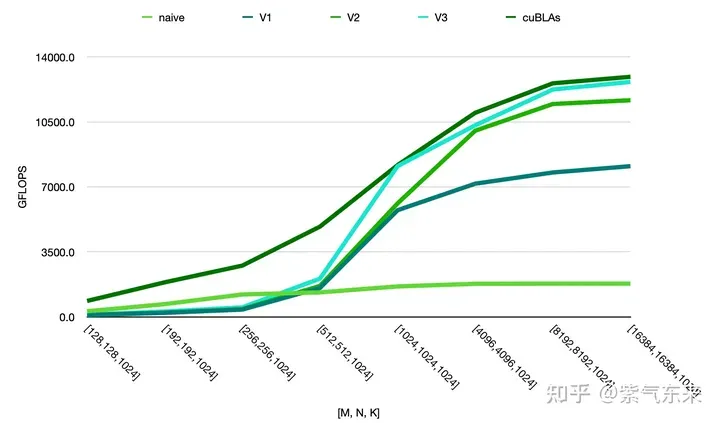
From this, we can compare the performance of the above methods. It can be seen that the performance of manual implementation is close to the official performance, as follows:


Editor in charge: Zhang YanniSource: The Heart of Autonomous Driving