Principle of spatiotemporal graph neural network and Pytorch implementation

In this interconnected world we live in, from microscopic molecular structures to macroscopic social networks to complex urban design structures, there are interconnected graphs of data hidden. These graph data are like mysterious nets, closely connecting everything in the world. As a revolutionary technology, graph neural network (GNN) is gradually unveiling these graph data with its powerful capabilities, allowing us to understand and utilize them more deeply.
The emergence of graph neural networks provides us with a new way of modeling and learning. It not only captures the spatial structure of data but also reveals complex relationships in graph structures. Whether in the field of biology, such as protein structure analysis and drug discovery, or in the field of sociology, such as social network simulation and public opinion analysis, graph neural networks have shown amazing application potential.
What’s even more exciting is that graph neural networks can also be integrated to form more powerful models. For example, combining a graph neural network with a sequence model to form a spatio-temporal graph neural network (Spatail-Temporal Graph) can not only capture the time and space dependencies of data, but also more comprehensively reveal the inherent laws and trends of the data. The emergence of this fusion model brings more possibilities to research and applications in various fields.
In spatiotemporal graph neural networks, the time dimension is cleverly introduced into the graph structure. This means that node characteristics that were originally stationary now change over time. This change not only reflects the dynamic relationship between nodes, but also provides us with richer information, allowing us to more accurately predict and analyze various complex phenomena.
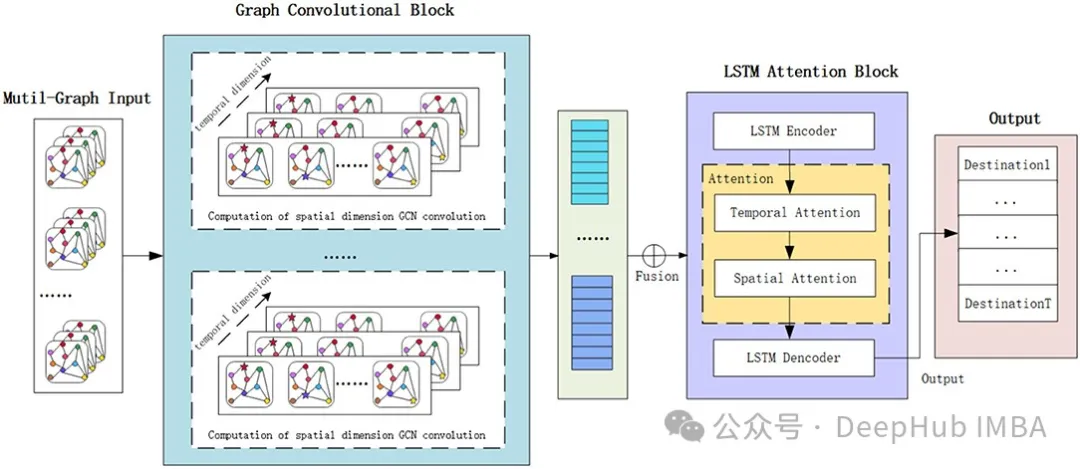
However, GNN models and sequence models (such as simple RNN, LSTM or GRU) are inherently complex. Combining these models to handle spatial and temporal dependencies is powerful, but also complex: difficult to understand and difficult to implement.
So in this article, we will delve into the principles of these models and implement a relatively simple example to gain a deeper understanding of their capabilities and applications.
Graph Neural Network (GNN)
Let’s first introduce some introductory knowledge and briefly discuss GNN.
A graph G can be defined as G = (V, E), where V is the set of nodes and E is the edge between them.
The feature matrix of a graph containing n nodes, each node with f features, is the connection of all features:
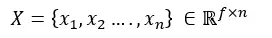
The key issue of GNN is the message passing between all connected nodes. This neighbor feature transformation and aggregation can be written as:

A is the adjacency matrix of the graph, and I is the identity matrix that allows self-connection. Although this is not a complete equation, it already illustrates the basis of graph convolutional networks that can learn spatial dependencies between different nodes. A classic graph neural network is shown below:

Spatio-temporal graph neural network (ST-GNN)
Each time step in ST-GNN is a graph and passed through the GCN/GAT network to obtain the resulting encoded graph embedding the spatial interdependencies of the data. These encoded graphs can then be modeled like time series data, as long as the integrity of the graph structure of the data for each time step is preserved. The figure below demonstrates these two steps. The temporal model can be any sequence model from ARIMA or a simple recurrent neural network or transformers.

We below use a simple recurrent neural network to draw the components of ST-GNN
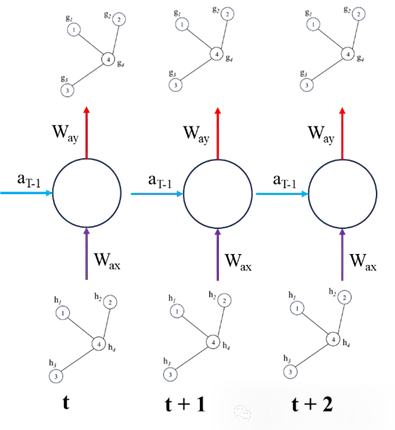
The above is the basic principle of ST-GNN, which combines GNN with sequence models (such as RNN, LSTM, GRU, Transformers, etc.). If you are already familiar with these sequences and GNN models, it is very simple in theory, but it will be a little complicated in actual operation, so we will directly use Pytorch to implement a simple ST-GNN below.
Pytorch implementation of ST-GNN
First things first: for the purposes of this demonstration I will be using stock market data for large technology companies. While these data are not graph data per se, such networks may capture the interdependencies between these companies, such that one company's performance (good or bad) may in turn affect the value of other companies in the market. But this is just a demonstration, and we do not recommend using ST-GNN in stock market prediction.
Load data and use yfinance directly to find everything.
import yfinance as yf
import datetime as dt
import pandas as pd
from sklearn.preprocessing import StandardScaler
import plotly.graph_objs as go
from plotly.offline import iplot
import matplotlib.pyplot as plt
############ Dataset download #################
start_date = dt.datetime(2013,1,1)
end_date = dt.datetime(2024,3,7)
#loading from yahoo finance
google = yf.download("GOOGL",start_date, end_date)
apple = yf.download("AAPL",start_date, end_date)
Microsoft = yf.download("MSFT", start_date, end_date)
Amazon = yf.download("AMZN", start_date, end_date)
meta = yf.download("META", start_date, end_date)
Nvidia = yf.download("NVDA", start_date, end_date)
data = pd.DataFrame({'google': google['Open'],'microsoft': Microsoft['Open'],'amazon': Amazon['Open'],
'Nvidia': Nvidia['Open'],'meta': meta['Open'], 'apple': apple['Open']})
############## Scaling data ######################
scaler = StandardScaler()
data_scaled = pd.DataFrame(scaler.fit_transform(data), columns=data.columns)- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- twenty one.
- twenty two.
- twenty three.
- twenty four.
In order to adapt to ST-GNN, we need to transform the data to adapt to the requirements of the model
Converting scalar time series datasets into graph data structures is a critical step in converting traditional data into a form that graph neural networks can process. The functions and classes described here are as follows:
- Definition of adjacency matrix : The AdjacencyMatrix function defines the adjacency matrix (connectivity) of a graph, which is usually done based on the structure of the physical system at hand. However, here, the authors only used an all-1 matrix, i.e. all nodes are connected to all other nodes.
- Stock Market Dataset Class : The StockMarketDataset class is designed to create datasets for training spatiotemporal graph neural networks (ST-GNNs). The methods contained in this class are:
- Data sequence generation : The DatasetCreate method generates a data sequence.
- Constructing graph edges : The _create_edges method constructs the edges of the graph using an adjacency matrix.
- Generate data sequences : The _create_sequences method generates data sequences by sliding the window on the input stock market data.
This data preparation code can be easily adapted to other problems. This includes defining how nodes are connected at each time step and using sliding window methods to extract sequence features that can be learned by the model. Through this method, originally simple time series data is transformed into a graph data structure with complex relationships and time dependencies, so that graph neural networks can be used for deeper analysis and prediction.
def AdjacencyMatrix(L):
AdjM = np.ones((L,L))
return AdjM
class StockMarketDataset:
def __init__(self, W,N_hist, N_pred):
self.W = W
self.N_hist = N_hist
self.N_pred = N_pred
def DatasetCreate(self):
num_days, self.n_node = data_scaled.shape
n_window = self.N_hist + self.N_pred
edge_index, edge_attr = self._create_edges(self.n_node)
sequences = self._create_sequences(data_scaled, self.n_node, n_window, edge_index, edge_attr)
return sequences
def _create_edges(self, n_node):
edge_index = torch.zeros((2, n_node**2), dtype=torch.long)
edge_attr = torch.zeros((n_node**2, 1))
num_edges = 0
for i in range(n_node):
for j in range(n_node):
if self.W[i, j] != 0:
edge_index[:, num_edges] = torch.tensor([i, j], dtype=torch.long)
edge_attr[num_edges, 0] = self.W[i, j]
num_edges += 1
edge_index = edge_index[:, :num_edges]
edge_attr = edge_attr[:num_edges]
return edge_index, edge_attr
def _create_sequences(self, data, n_node, n_window, edge_index, edge_attr):
sequences = []
num_days, _ = data.shape
for i in range(num_days):
sta = i
end = i+n_window
full_window = np.swapaxes(data[sta:end, :], 0, 1)
g = Data(x=torch.FloatTensor(full_window[:, :self.N_hist]),
y=torch.FloatTensor(full_window[:, self.N_hist:]),
edge_index=edge_index,
num_nodes=n_node)
sequences.append(g)
return sequences- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- twenty one.
- twenty two.
- twenty three.
- twenty four.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
Train-validate-test split.
from torch_geometric.loader import DataLoader
def train_val_test_splits(sequences, splits):
total = len(sequences)
split_train, split_val, split_test = splits
# Calculate split indices
idx_train = int(total * split_train)
idx_val = int(total * (split_train + split_val))
indices = [i for i in range(len(sequences)-100)]
random.shuffle(indices)
train = [sequences[index] for index in indices[:idx_train]]
val = [sequences[index] for index in indices[idx_train:idx_val]]
test = [sequences[index] for index in indices[idx_val:]]
return train, val, test
'''Setting up the hyper paramaters'''
n_nodes = 6
n_hist = 50
n_pred = 10
batch_size = 32
# Adjacency matrix
W = AdjacencyMatrix(n_nodes)
# transorm data into graphical time series
dataset = StockMarketDataset(W, n_hist, n_pred)
sequences = dataset.DatasetCreate()
# train, validation, test split
splits = (0.9, 0.05, 0.05)
train, val, test = train_val_test_splits(sequences, splits)
train_dataloader = DataLoader(train, batch_size=batch_size, shuffle=True, drop_last = True)
val_dataloader = DataLoader(val, batch_size=batch_size, shuffle=True, drop_last=True)
test_dataloader = DataLoader(test, batch_size=batch_size, shuffle=True, drop_last = True)- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- twenty one.
- twenty two.
- twenty three.
- twenty four.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
Our model includes a GATConv and 2 GRU layers as encoders, and 1 GRU layer + fully connected layer as decoders. GATconv is the GNN part that can capture spatial dependence, and the GRU layer can capture the temporal dynamics of the data. The code includes a lot of data reshaping to ensure that the input dimensions of each layer are the same. This is also what we call the most complex part of the ST-GNN implementation, so if you want to know specifically the dimensions of the input to each layer, you can print the shape of x at different stages of the forward pass and compare it with the GRU and Linear layers. Documents of expected input dimensions are compared.
import torch
import torch.nn.functional as F
from torch_geometric.nn import GATConv
class ST_GNN_Model(torch.nn.Module):
def __init__(self, in_channels, out_channels, n_nodes,gru_hs_l1, gru_hs_l2, heads=1, dropout=0.01):
super(ST_GAT, self).__init__()
self.n_pred = out_channels
self.heads = heads
self.dropout = dropout
self.n_nodes = n_nodes
self.gru_hidden_size_l1 = gru_hs_l1
self.gru_hidden_size_l2 = gru_hs_l2
self.decoder_hidden_size = self.gru_hidden_size_l2
# enconder GRU layers
self.gat = GATConv(in_channels=in_channels, out_channels=in_channels,
heads=heads, dropout=dropout, cnotallow=False)
self.encoder_gru_l1 = torch.nn.GRU(input_size=self.n_nodes,
hidden_size=self.gru_hidden_size_l1, num_layers=1,
bias = True)
self.encoder_gru_l2 = torch.nn.GRU(input_size=self.gru_hidden_size_l1,
hidden_size=self.gru_hidden_size_l2, num_layers = 1,
bias = True)
self.GRU_decoder = torch.nn.GRU(input_size = self.gru_hidden_size_l2, hidden_size = self.decoder_hidden_size,
num_layers =1, bias = True, dropout= self.dropout)
self.prediction_layer = torch.nn.Linear(self.decoder_hidden_size, self.n_nodes*self.n_pred, bias= True)
def forward(self, data, device):
x, edge_index = data.x, data.edge_index
if device == 'cpu':
x = torch.FloatTensor(x)
else:
x = torch.cuda.FloatTensor(x)
x = self.gat(x, edge_index)
x = F.dropout(x, self.dropout, training=self.training)
batch_size = data.num_graphs
n_node = int(data.num_nodes / batch_size)
x = torch.reshape(x, (batch_size, n_node, data.num_features))
x = torch.movedim(x, 2, 0)
encoderl1_outputs, _ = self.encoder_gru_l1(x)
x = F.relu(encoderl1_outputs)
encoderl2_outputs, h2 = self.encoder_gru_l2(x)
x = F.relu(encoderl2_outputs)
x, _ = self.GRU_decoder(x,h2)
x = torch.squeeze(x[-1,:,:])
x = self.prediction_layer(x)
x = torch.reshape(x, (batch_size, self.n_nodes, self.n_pred))
x = torch.reshape(x, (batch_size*self.n_nodes, self.n_pred))
return x- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- twenty one.
- twenty two.
- twenty three.
- twenty four.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
The training process is almost the same as any network training process in pytorch.
import torch
import torch.optim as optim
# Hyperparameters
gru_hs_l1 = 16
gru_hs_l2 = 16
learning_rate = 1e-3
Epochs = 50
device = 'cuda' if torch.cuda.is_available() else 'cpu'
model = ST_GNN_Model(in_channels=n_hist, out_channels=n_pred, n_nodes=n_nodes, gru_hs_l1=gru_hs_l1, gru_hs_l2 = gru_hs_l2)
pretrained = False
model_path = "ST_GNN_Model.pth"
if pretrained:
model.load_state_dict(torch.load(model_path))
optimizer = optim.Adam(model.parameters(), lr=learning_rate, weight_decay=1e-7)
criterion = torch.nn.MSELoss()
model.to(device)
for epoch in range(Epochs):
model.train()
for _, batch in enumerate(tqdm(train_dataloader, desc=f"Epoch {epoch}")):
batch = batch.to(device)
optimizer.zero_grad()
y_pred = torch.squeeze(model(batch, device))
loss= criterion(y_pred.float(), torch.squeeze(batch.y).float())
loss.backward()
optimizer.step()
print(f"Loss: {loss:.7f}")- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- twenty one.
- twenty two.
- twenty three.
- twenty four.
- 25.
- 26.
- 27.
- 28.
After the model training is completed, let’s visualize the prediction ability of the model. For each data input, the code below predicts the model output and then plots the model output against the ground truth.
@torch.no_grad()
def Extract_results(model, device, dataloader, type=''):
model.eval()
model.to(device)
n = 0
# Evaluate model on all data
for i, batch in enumerate(dataloader):
batch = batch.to(device)
if batch.x.shape[0] == 1:
pass
else:
with torch.no_grad():
pred = model(batch, device)
truth = batch.y.view(pred.shape)
if i == 0:
y_pred = torch.zeros(len(dataloader), pred.shape[0], pred.shape[1])
y_truth = torch.zeros(len(dataloader), pred.shape[0], pred.shape[1])
y_pred[i, :pred.shape[0], :] = pred
y_truth[i, :pred.shape[0], :] = truth
n += 1
y_pred_flat = torch.reshape(y_pred, (len(dataloader),batch_size,n_nodes,n_pred))
y_truth_flat = torch.reshape(y_truth,(len(dataloader),batch_size,n_nodes,n_pred))
return y_pred_flat, y_truth_flat
def plot_results(predictions,actual, step, node):
predictions = torch.tensor(predictions[:,:,node,step]).squeeze()
actual = torch.tensor(actual[:,:,node,step]).squeeze()
pred_values_float = torch.reshape(predictions,(-1,))
actual_values_float = torch.reshape(actual, (-1,))
scatter_trace = go.Scatter(
x=actual_values_float,
y=pred_values_float,
mode='markers',
marker=dict(
size=10,
opacity=0.5,
color='rgba(255,255,255,0)',
line=dict(
width=2,
color='rgba(152, 0, 0, .8)',
)
),
name='Actual vs Predicted'
)
line_trace = go.Scatter(
x=[min(actual_values_float), max(actual_values_float)],
y=[min(actual_values_float), max(actual_values_float)],
mode='lines',
marker=dict(color='blue'),
name='Perfect Prediction'
)
data = [scatter_trace, line_trace]
layout = dict(
title='Actual vs Predicted Values',
xaxis=dict(title='Actual Values'),
yaxis=dict(title='Predicted Values'),
autosize=False,
width=800,
height=600
)
fig = dict(data=data, layout=layout)
iplot(fig)
y_pred, y_truth = Extract_results(model, device, test_dataloader, 'Test')
plot_results(y_pred, y_truth,9,0) # timestep, node- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- twenty one.
- twenty two.
- twenty three.
- twenty four.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
- 61.
- 62.
- 63.
- 64.
For 6 nodes (companies), given the past 50 values, 10 predictions are made. Below is a plot of the 10th step prediction versus the true value for the first node. Just because it looks good, doesn't necessarily mean it's great. Because for time series data, the best estimator of the next value is always the previous value. If not well trained, these models can output values similar to the last value of the input data, rather than capturing temporal dynamics.

For a given node, we can plot historical inputs, predictions, and ground truth to compare and see if the predictions capture the pattern.
@torch.no_grad()
def forecastModel(model, device, dataloader, node):
model.eval()
model.to(device)
for i, batch in enumerate(dataloader):
batch = batch.to(device)
with torch.no_grad():
pred = model(batch, device)
truth = batch.y.view(pred.shape)
# the shape should [batch_size, nodes, number of predictions]
truth = torch.reshape(truth, [batch_size, n_nodes,n_pred])
pred = torch.reshape(pred, [batch_size, n_nodes,n_pred])
x = batch.x
x = torch.reshape(x, [batch_size, n_nodes,n_hist])
y_pred = torch.squeeze(pred[0, node, :])
y_truth = torch.squeeze(truth[0,node,:])
y_past = torch.squeeze(x[0, node, :])
t_range = [t for t in range(len(y_past))]
break
t_shifted = [t_range[-1]+1+t for t in range(len(y_pred))]
trace1 = go.Scatter(x =t_range, y= y_past, mode = "markers", name = "Historical data")
trace2 = go.Scatter(x=t_shifted, y=y_pred, mode = "markers", name = "pred")
trace3 = go.Scatter(x=t_shifted, y=y_truth, mode = "markers", name = "truth")
layout = go.Layout(title = "forecasting", xaxis=dict(title = 'time'),
yaxis=dict(title = 'y-value'), width = 1000, height = 600)
figure = go.Figure(data = [trace1, trace2, trace3], layout = layout)
iplot(figure)
forecastModel(model, device, test_dataloader, 0)- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- twenty one.
- twenty two.
- twenty three.
- twenty four.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.

The predictions of the first node (Google) at 4 different points on the test data set were actually better than I thought, the others didn't seem so great.
Summarize
My understanding is that future stock prices cannot be predicted by pure historical value autoregression because stocks are determined by real-world events, which are not reflected in historical values. This is why we said earlier that it is not recommended to use ST-GNN in stock market prediction. We use this data set just because it is easy to obtain. Finally, don’t forget to focus on the purpose of our article, learn the basic concepts of ST-GNN, and understand the working principle of ST-GNN through Pytorch code implementation.