Diffusion model overcomes algorithmic problems, AGI is not far away! Google Brain finds the shortest path in a maze
Can the "diffusion model" also overcome algorithmic problems?
picture
A PhD researcher conducted an interesting experiment using "discrete diffusion" to find the shortest path in a maze represented by an image.
picture
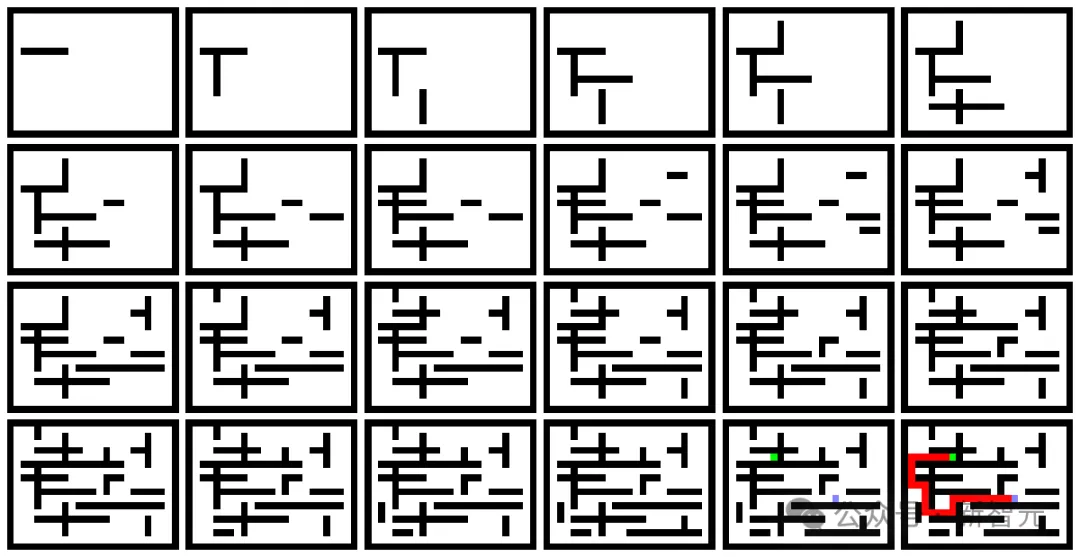
According to the author, each maze is generated by repeatedly adding horizontal and vertical walls.
Among them, the starting point and target point are randomly selected.
Randomly sample a path as the solution from the shortest path from the starting point to the target point. The shortest path is calculated using an exact algorithm.
picture
Then use discrete diffusion model and U-Net.
The maze with start and goal is encoded in one channel, and the model uses the solution in another channel to de-noise the maze.
picture
Even a more difficult maze can be done well.
picture
To estimate the denoising step p(x_{t-1} | x_t), the algorithm estimates p(x_0 | x_t). Visualizing this estimate (bottom row) during the process shows the "current assumptions" and ultimately focuses on the results.
picture
NVIDIA senior scientist Jim Fan said that this is an interesting experiment, and the diffusion model can "render" the algorithm. It can implement maze traversal from pixels only, even using U-Net, which is much weaker than Transforme.
I've always thought of the diffusion model as the renderer, and the Transformer as the inference engine. It seems that the renderer itself can also encode very complex sequential algorithms.
picture
This experiment simply shocked netizens, "What else can the diffusion model do?!"
picture
Others say that AGI will be solved once someone trains the Diffusion Transformer on a good enough data set.
picture
However, this research has not yet been officially released, and the author stated that it will be updated on arxiv later.
It is worth mentioning that in this experiment, they used the discrete diffusion model proposed by the Google Brain team in 2021.
picture
Just recently, the study was given an updated version.
discrete diffusion model
"Generative model" is the core problem in machine learning.
It can be used both as a measure of our ability to capture statistics on natural datasets and in downstream applications that need to generate high-dimensional data such as images, text, and speech.
Methods such as GAN, VAE, large autoregressive neural network models, and normalized flow all have their own advantages and disadvantages in terms of sample quality, sampling speed, log likelihood, and training stability.
Recently, the "diffusion model" has become the most popular alternative for image and audio generation.
It can achieve sample quality comparable to GAN and log-likelihood comparable to autoregressive models with fewer inference steps.
picture
Paper address: https://arxiv.org/pdf/2107.03006.pdf
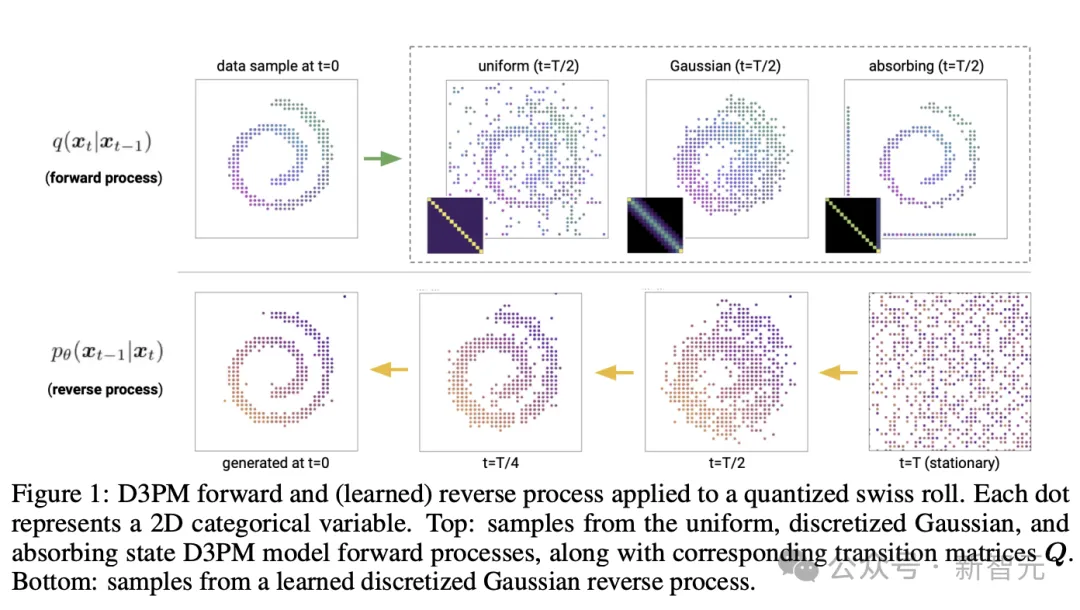
Although diffusion models for discrete and continuous state spaces have been proposed, recent research has mainly focused on Gaussian diffusion processes operating in continuous state spaces (such as real-valued images and waveform data).
Discrete state space diffusion models have been explored in the field of text and image segmentation, but have not yet proven to be a competitive model in large-scale generation tasks of text and images.
The Google research team proposed a new discrete denoising diffusion probability model (D3PM).
In the study, the authors demonstrate that the choice of overmatrix is an important design decision that can improve results in both image and text domains.
Furthermore, they propose a new loss function that combines a variational lower bound and an auxiliary cross-entropy loss.
In terms of text, this model achieves good results in character-level text generation while being scalable to the large-vocabulary LM1B dataset.
On the CIFAR-10 image dataset, the latest model approaches the sample quality of the continuous-space DDPM model and exceeds the log-likelihood of the continuous-space DDPM model.
picture
Project author
Arnaud Pannatier
Arnaud Pannatier started studying for his PhD in March 2020 in the machine learning group of his supervisor François Fleuret.
He recently developed HyperMixer, which uses a super network to enable MLPMixer to handle inputs of various lengths. This enables the model to process the input in a permutation-invariant manner and has been shown to give the model an attentional behavior that scales linearly with the length of the input.
At EPFL, he earned a bachelor's degree in physics and a master's degree in computer science and engineering (CSE-MASH).