From theory to implementation, implement the Focus network hand-in-hand

From theory to implementation, implement the Focus network hand-in-hand
Author | Liang Tang
Produced | Official number: Coder Liang (ID: Coder_LT)
Hello everyone, I'm Lao Liang.
We previously introduced the core of Transformer, the attention network, but we only introduced its principles and did not explain its implementation in detail. Just talking about the theory inevitably seems a bit empty, so let's talk about its implementation.
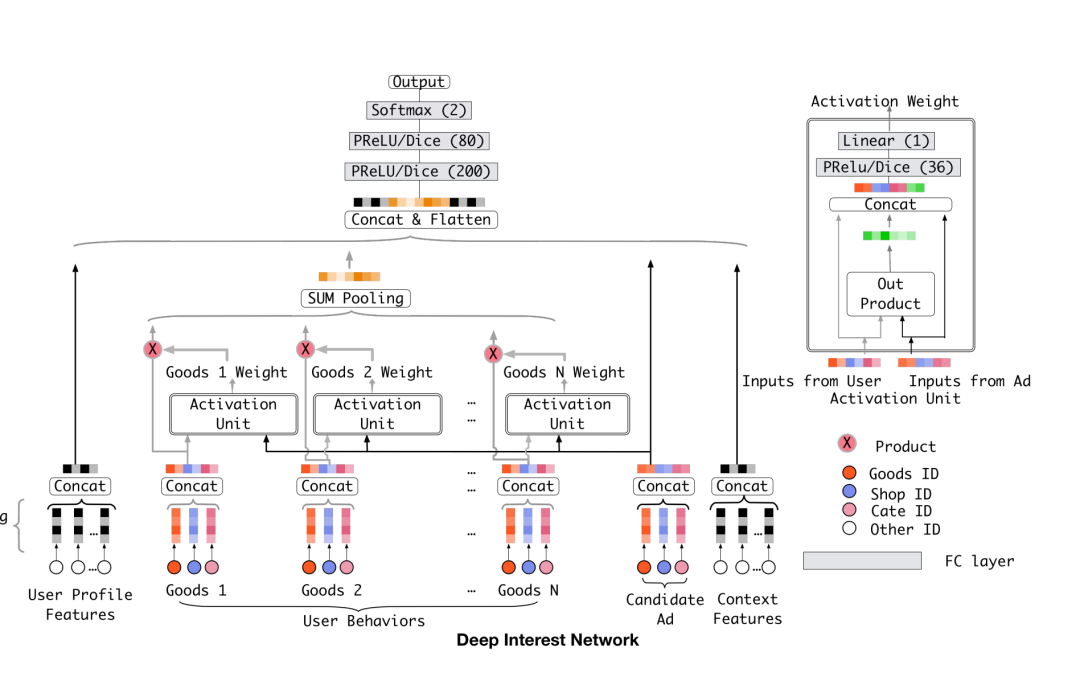
In order to help you better understand, here I chose the DIN model in the e-commerce scene as an entry point.
On the one hand, it can help everyone understand how the ordering of goods in the recommendation and advertising systems in the current e-commerce system is done, and I personally feel that DIN is easier to understand than directly nibbling on the transformer.
We can start with the data of the attention network, which has two input data: one is the user's historical behavior sequence, and the other is the item to be scored (hereinafter referred to as the target item). The user's historical behavior sequence is essentially an array of items that the user has interacted with in history. Here, for the sake of simplification, we assume that the conversion from item to embedding has been completed.
The first is the target item, whose shape should be [B, E]. B here refers to batch_size, that is, the size of a batch at training time. The E here refers to the length of embedding. There are also some articles that use other letters to indicate this, which does not have a hard standard, just understand it.
Let's look at the user behavior sequence, in addition to the batch_size and embedding length, an additional parameter is needed to indicate the length of the behavior sequence, usually we use the letter T. For all samples, we need to ensure that its behavior sequence length is T, and if it is less than T, it is made up with the default value. If T's are exceeded, truncation is performed. Thus, its shape should be [B, T, E].
According to the principle of attention network, we need to calculate the weight according to the similarity of each item in the behavior sequence to the target item. Finally, the embedding of this T item is weighted and summed. After summing, the T items are combined according to the calculated weights to obtain an embedding. The paper says that this embedding that integrates T behavioral sequences is the expression of user interest, and we only need to splice it with the target item and send it to the neural network, which can help the model make better decisions. Here the shape of the user's interest should be the same as the item, which is also [B, E].
To summarize briefly, we now need a module that receives two inputs, one for the embedding of the item and one for the embedding of the user's behavior sequence. Its output should be [B, T], corresponding to the weights of T items in the sequence of behaviors. The remaining question is how to generate this result.
After the principle, let's talk about implementation, we can combine the structure diagram in the following two papers to help understand.
 Image
Image
First, let's unify the input dimensions and manually turn the two-dimensional vector of item embedding into three dimensions, that is, shape into [B, 1, E].
Here, one method is to manually loop T times, take an item embedding from the behavior sequence each time, and stitch it with the embedding of the target item and throw it into a neural network to get a score.
This approach is very disrecommended, generally in neural networks, we are not a last resort, do not manually loop, because the loop is linear calculation, there is no way to use the GPU parallel computing to accelerate.
For the current problem, we can completely use matrix operations instead. By using the expand/tile function, the item embedding of [B, 1, E] is duplicated in T parts, and the shape becomes [B, T, E]. In this way, the shape of both inputs becomes [B, T, E], and we can stitch them together to become [B, T, 2E].
Then go through a neural network with an input of 2E and an output of 1, and finally get the result of [B, T, 1], we switch the dimension and become [B, 1, T], which is the weight we want.
Here I found a copy of Pytorch's code, let's substitute the above logic to see, it should not be difficult to understand.
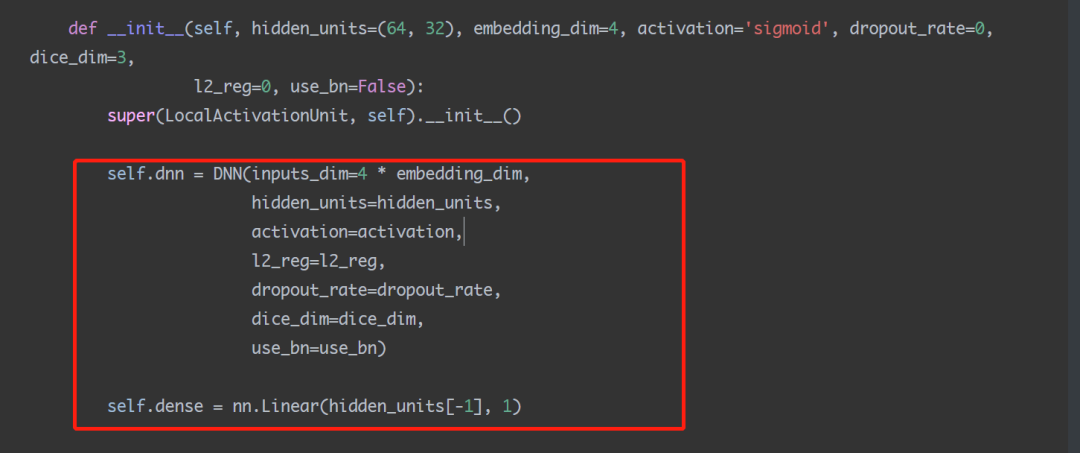
class LocalActivationUnit(nn. Module):
def __init__(self, hidden_units=(64, 32), embedding_dim=4, activation='sigmoid', dropout_rate=0, dice_dim=3,
l2_reg=0, use_bn=False):
super(LocalActivationUnit, self).__init__()
self.dnn = DNN(inputs_dim=4 * embedding_dim,
hidden_units=hidden_units,
activation=activation,
l2_reg=l2_reg,
dropout_rate=dropout_rate,
dice_dim=dice_dim,
use_bn=use_bn)
self.dense = nn.Linear(hidden_units[-1], 1)- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
def forward(self, query, user_behavior): # query ad : size -> batch_size * 1 * embedding_size # user behavior : size -> batch_size * time_seq_len * embedding_size user_behavior_len = user_behavior.size(1)
queries = query.expand(-1, user_behavior_len, -1)
attention_input = torch.cat([queries, user_behavior, queries - user_behavior, queries * user_behavior],
dim=-1) # as the source code, subtraction simulates verctors' difference
attention_output = self.dnn(attention_input)
attention_score = self.dense(attention_output) # [B, T, 1]
return attention_score- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
In fact, this piece of code is the core of the attention network, which generates the most important weight in attention. Once the weight is available, we only need to multiply it by the embedding of the user's behavior sequence. Taking advantage of the properties of matrix multiplication, a [B, 1. Multiplying the matrix of T] by a matrix of [B, T, E] gives the result of [B, 1, E]. The result of this multiplication is actually the weighted sum we need, but it is achieved by matrix multiplication.
Let's take a look at the source code again to deepen our understanding:
class AttentionSequencePoolingLayer(nn. Module): """The Attentional sequence pooling operation used in DIN & DIEN.
Arguments
- **att_hidden_units**:list of positive integer, the attention net layer number and units in each layer.
- **att_activation**: Activation function to use in attention net.
- **weight_normalization**: bool.Whether normalize the attention score of local activation unit.
- **supports_masking**:If True,the input need to support masking.
References
- [Zhou G, Zhu X, Song C, et al. Deep interest network for click-through rate prediction[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM, 2018: 1059-1068.](https://arxiv.org/pdf/1706.06978.pdf)
"""
def __init__(self, att_hidden_units=(80, 40), att_activation='sigmoid', weight_normalization=False,
return_score=False, supports_masking=False, embedding_dim=4, **kwargs):
super(AttentionSequencePoolingLayer, self).__init__()
self.return_score = return_score
self.weight_normalization = weight_normalization
self.supports_masking = supports_masking
self.local_att = LocalActivationUnit(hidden_units=att_hidden_units, embedding_dim=embedding_dim,
activation=att_activation,
dropout_rate=0, use_bn=False)- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
[docs] def forward(self, query, keys, keys_length, mask=None): """ Input shape - A list of three tensor: [query,keys,keys_length]
- query is a 3D tensor with shape: ``(batch_size, 1, embedding_size)``
- keys is a 3D tensor with shape: ``(batch_size, T, embedding_size)``
- keys_length is a 2D tensor with shape: ``(batch_size, 1)``
Output shape
- 3D tensor with shape: ``(batch_size, 1, embedding_size)``.
"""
batch_size, max_length, _ = keys.size()
# Mask
if self.supports_masking:
if mask is None:
raise ValueError("When supports_masking=True,input must support masking")
keys_masks = mask.unsqueeze(1)
else:
keys_masks = torch.arange(max_length, device=keys_length.device, dtype=keys_length.dtype).repeat(batch_size,1) # [B, T]
keys_masks = keys_masks < keys_length.view(-1, 1) # 0, 1 mask
keys_masks = keys_masks.unsqueeze(1) # [B, 1, T]
attention_score = self.local_att(query, keys) # [B, T, 1]
outputs = torch.transpose(attention_score, 1, 2) # [B, 1, T]
if self.weight_normalization:
paddings = torch.ones_like(outputs) * (-2 ** 32 + 1)
else:
paddings = torch.zeros_like(outputs)
outputs = torch.where(keys_masks, outputs, paddings) # [B, 1, T]
# Scale
# outputs = outputs / (keys.shape[-1] ** 0.05)
if self.weight_normalization:
outputs = F.softmax(outputs, dim=-1) # [B, 1, T]
if not self.return_score:
# Weighted sum
outputs = torch.matmul(outputs, keys) # [B, 1, E]
return outputs- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
This code adds mask and normalization and other logic, if all ignored, the real core trunk code is only three lines:
attention_score = self.local_att(query, keys) # [B, T, 1] outputs = torch.transpose(attention_score, 1, 2) # [B, 1, T] outputs = torch.matmul(outputs, keys) # [B, 1, E] At this point, even if we have finished talking about the implementation method of attention network, we have almost understood the DIN paper, but there is one more detail worth talking about. It's about the weight of attention.
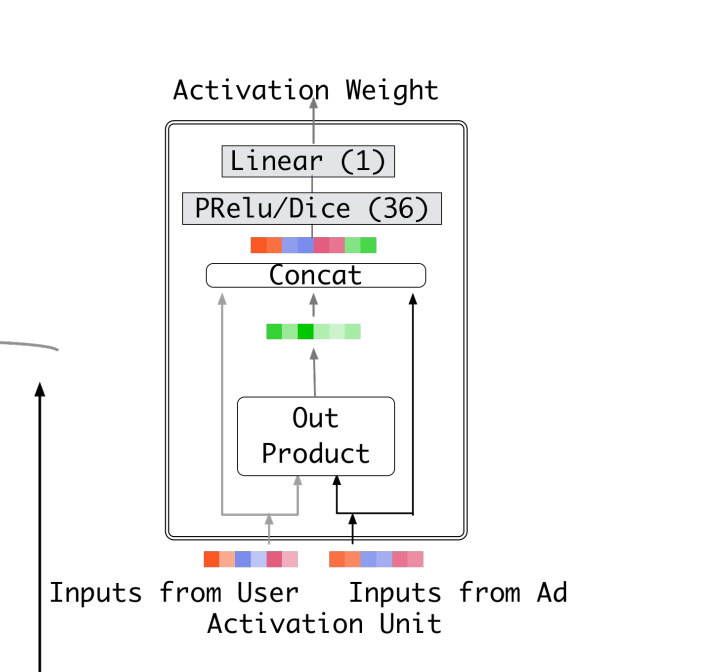
In the DIN paper, we used a separate LocalActivationUnit to learn the weights of the two embeddings spliced, which is the part of the code above:
 Image
Image
We give weights to two vectors by scoring them through a separate neural network, and the logic of this weight is not necessarily calculated based on the similarity of the vectors. After all, neural networks are a black box, and we can't guess the internal logic. It's just that logically or empirically, we prefer that it is calculated based on the similarity of vectors.
There is also a attention structure in the Transformer, which is calculated using the similarity between vectors. As a matter of common sense, calculating weights according to vector similarity should be easier to understand. But that's not necessarily the way you feel during the learning process, which is why I shared DIN first instead of going directly to transformer self-attention.