从理论到实现,手把手实现Attention网络

从理论到实现,手把手实现Attention网络
作者 | 梁唐
出品 | 公众号:Coder梁(ID:Coder_LT)
大家好,我是老梁。
我们之前介绍了Transformer的核心——attention网络,我们之前只是介绍了它的原理,并且没有详细解释它的实现方法。光聊理论难免显得有些空洞,所以我们来谈谈它的实现。
为了帮助大家更好地理解, 这里我选了电商场景中的DIN模型来做切入点。
一方面可以帮助大家理解现在电商系统中的推荐和广告系统中的商品排序都是怎么做的,另外我个人感觉DIN要比直接去硬啃transformer容易理解一些。
我们可以先从attention网络的数据入手,它的输入数据有两个:一个是用户的历史行为序列,一个是待打分的item(以下称为target item)。用户的历史行为序列本质上其实就是一个用户历史上有过交互的item的数组。这里为了简化,我们假设已经完成了从item到embedding的转换。
首先是target item,它的shape应该是[B, E]。这里的B指的是batch_size,即训练时候一个批量的大小。这里的E指的是embedding的长度。也有一些文章里使用别的字母表示,这也没有一个硬性的标准,能看懂就行。
我们再来看用户行为序列,除了batch_size和embedding长度之外,还需要一个额外的参数来表示行为序列的长度,通常我们用字母T。对于所有的样本,我们都需要保证它的行为序列长度是T,如果不足T的,则使用默认值补足。如果超过T的,则进行截断。如此,它的shape应该是[B, T, E]。
根据attention网络的原理,我们需要根据行为序列中的每个item与target item的相似度,再根据相似度计算权重。最后对这T个item的embedding进行加权求和。求和之后,这T个item根据计算得到的权重合并得到一个embedding。论文中说这个集成T个行为序列的embedding就是用户兴趣的表达,我们只需要将它和目标item拼接在一起发送到神经网络即可,就可以帮助模型更好地决策了。这里用户兴趣的shape应该和item是一样的,也是[B, E]。
简单总结一下,我们现在需要一个模块,它接收两个输入,一个是item的embedding,一个是用户行为序列的embedding。它的输出应该是[B, T],对应行为序列中T个item的权重。剩下的问题就是怎么生成这个结果。
原理讲完了,接下来讲讲实现,我们可以结合一下下面这两张论文中的结构图帮助理解。
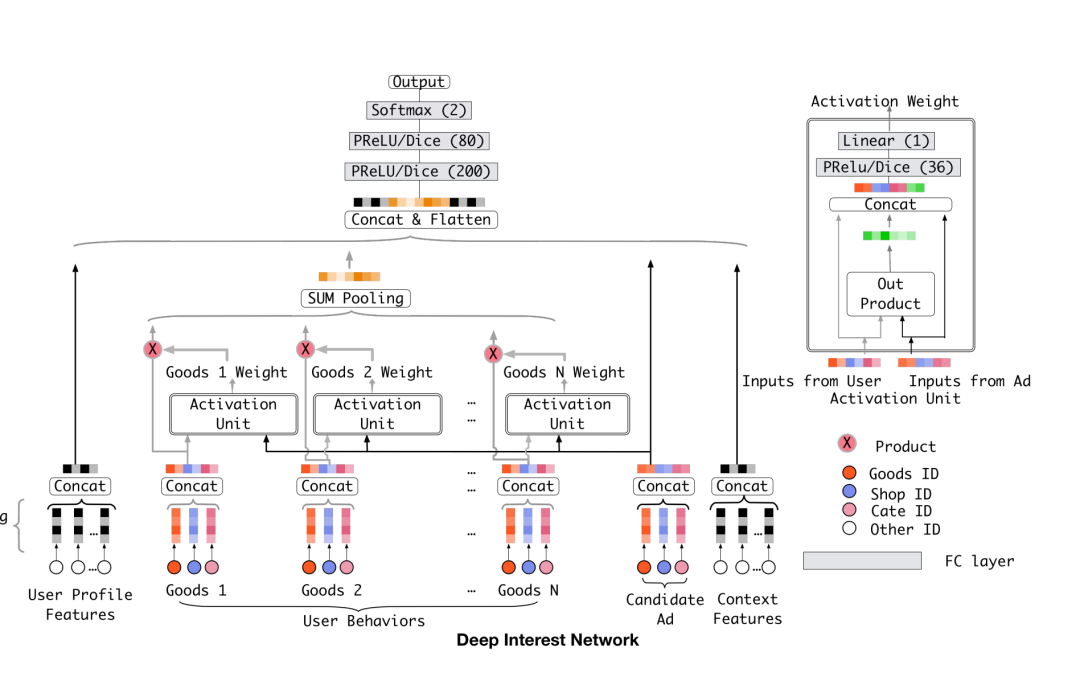
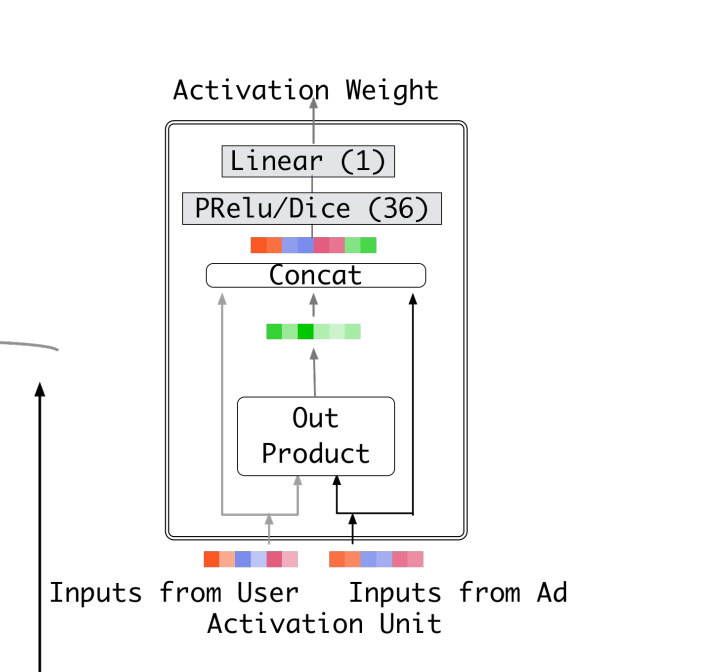 图片
图片
首先,我们来统一一下输入的维度,手动将item的embedding这个二维的向量变成三维,即shape变成[B, 1, E]。
这里一种做法是,手动循环T次,每次从行为序列中拿出一个item embedding,和目标item的embedding拼接在一起丢进一个神经网络中得到一个分数。
这种做法非常不推荐,一般在神经网络当中,我们不到万不得已,不手动循环,因为循环是线性计算,没办法利用GPU的并行计算来加速。
对于当前问题来说,我们完全可以使用矩阵运算来代替。通过使用expand/tile函数,将[B, 1, E]的item embedding复制T份,形状也变成[B, T, E]。这样一来,两个输入的shape都变成了[B, T, E],我们就可以把它们拼接到一起变成[B, T, 2E]。
然后经过一个输入是2E,输出是1的神经网络,最终得到[B, T, 1]的结果,我们把它调换一下维度,变成[B, 1, T],这个就是我们想要的权重了。
这里我找来一份Pytorch的代码,大家代入一下上面的逻辑去看一下,应该不难看懂。
class LocalActivationUnit(nn.Module):
def __init__(self, hidden_units=(64, 32), embedding_dim=4, activation='sigmoid', dropout_rate=0, dice_dim=3,
l2_reg=0, use_bn=False):
super(LocalActivationUnit, self).__init__()
self.dnn = DNN(inputs_dim=4 * embedding_dim,
hidden_units=hidden_units,
activation=activation,
l2_reg=l2_reg,
dropout_rate=dropout_rate,
dice_dim=dice_dim,
use_bn=use_bn)
self.dense = nn.Linear(hidden_units[-1], 1)- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
def forward(self, query, user_behavior): # query ad : size -> batch_size * 1 * embedding_size # user behavior : size -> batch_size * time_seq_len * embedding_size user_behavior_len = user_behavior.size(1)
queries = query.expand(-1, user_behavior_len, -1)
attention_input = torch.cat([queries, user_behavior, queries - user_behavior, queries * user_behavior],
dim=-1) # as the source code, subtraction simulates verctors' difference
attention_output = self.dnn(attention_input)
attention_score = self.dense(attention_output) # [B, T, 1]
return attention_score- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
其实这一段代码就是attention网络的核心,它生成的是attention中最重要的权重。权重有了之后,我们只需要将它和用户行为序列的embedding相乘。利用矩阵乘法的特性,一个[B, 1. T]的矩阵乘上一个[B, T, E]的矩阵,会得到[B, 1, E]的结果。这个相乘之后的结果其实就是我们需要的加权求和,只不过是通过矩阵乘法来实现了。
我们再看下源码加深一下理解:
class AttentionSequencePoolingLayer(nn.Module): """The Attentional sequence pooling operation used in DIN & DIEN.
Arguments
- **att_hidden_units**:list of positive integer, the attention net layer number and units in each layer.
- **att_activation**: Activation function to use in attention net.
- **weight_normalization**: bool.Whether normalize the attention score of local activation unit.
- **supports_masking**:If True,the input need to support masking.
References
- [Zhou G, Zhu X, Song C, et al. Deep interest network for click-through rate prediction[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM, 2018: 1059-1068.](https://arxiv.org/pdf/1706.06978.pdf)
"""
def __init__(self, att_hidden_units=(80, 40), att_activation='sigmoid', weight_normalization=False,
return_score=False, supports_masking=False, embedding_dim=4, **kwargs):
super(AttentionSequencePoolingLayer, self).__init__()
self.return_score = return_score
self.weight_normalization = weight_normalization
self.supports_masking = supports_masking
self.local_att = LocalActivationUnit(hidden_units=att_hidden_units, embedding_dim=embedding_dim,
activation=att_activation,
dropout_rate=0, use_bn=False)- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
[docs] def forward(self, query, keys, keys_length, mask=None): """ Input shape - A list of three tensor: [query,keys,keys_length]
- query is a 3D tensor with shape: ``(batch_size, 1, embedding_size)``
- keys is a 3D tensor with shape: ``(batch_size, T, embedding_size)``
- keys_length is a 2D tensor with shape: ``(batch_size, 1)``
Output shape
- 3D tensor with shape: ``(batch_size, 1, embedding_size)``.
"""
batch_size, max_length, _ = keys.size()
# Mask
if self.supports_masking:
if mask is None:
raise ValueError("When supports_masking=True,input must support masking")
keys_masks = mask.unsqueeze(1)
else:
keys_masks = torch.arange(max_length, device=keys_length.device, dtype=keys_length.dtype).repeat(batch_size,1) # [B, T]
keys_masks = keys_masks < keys_length.view(-1, 1) # 0, 1 mask
keys_masks = keys_masks.unsqueeze(1) # [B, 1, T]
attention_score = self.local_att(query, keys) # [B, T, 1]
outputs = torch.transpose(attention_score, 1, 2) # [B, 1, T]
if self.weight_normalization:
paddings = torch.ones_like(outputs) * (-2 ** 32 + 1)
else:
paddings = torch.zeros_like(outputs)
outputs = torch.where(keys_masks, outputs, paddings) # [B, 1, T]
# Scale
# outputs = outputs / (keys.shape[-1] ** 0.05)
if self.weight_normalization:
outputs = F.softmax(outputs, dim=-1) # [B, 1, T]
if not self.return_score:
# Weighted sum
outputs = torch.matmul(outputs, keys) # [B, 1, E]
return outputs- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
这段代码当中加入了mask以及normalization等逻辑,全部忽略掉的话,真正核心的主干代码就只有三行:
attention_score = self.local_att(query, keys) # [B, T, 1] outputs = torch.transpose(attention_score, 1, 2) # [B, 1, T] outputs = torch.matmul(outputs, keys) # [B, 1, E] 到这里我们关于attention网络的实现方法就算是讲完了,对于DIN这篇论文也就理解差不多了,不过还有一个细节值得聊聊。就是关于attention权重的问题。
在DIN这篇论文当中,我们是使用了一个单独的LocalActivationUnit来学习的两个embedding拼接之后的权重,也就是上图代码当中这个部分:
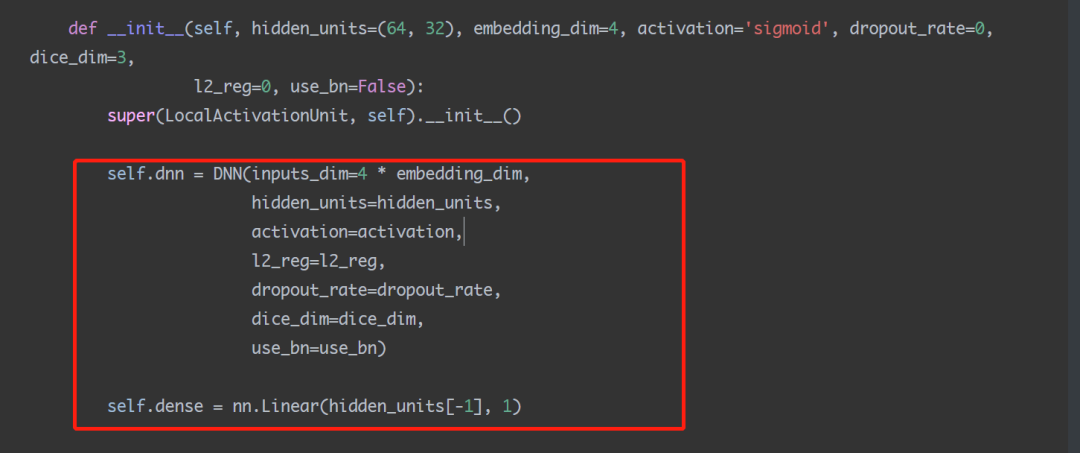 图片
图片
我们通过一个单独的神经网络来对两个向量打分给出权重,这个权重的运算逻辑并不一定是根据向量的相似度来计算的。毕竟神经网络是一个黑盒,我们无从猜测内部逻辑。只不过从逻辑上或者经验上来说,我们更倾向于它是根据向量的相似度来计算的。
而Transformer当中也有attention结构,它就是正儿八经地利用向量之间的相似度来计算的。常理上来说,按照向量相似度来计算权重,这种做法应该更容易理解一些。但实际上学习的过程当中的感受却并不一定如此,这也是为什么我先来分享DIN而不是直接上transformer self-attention的原因。