時空圖神經網路原理及Pytorch實現

在我們所處的這個充滿連結的世界中,從微觀的分子結構到宏觀的社交網絡,再到複雜的城市設計結構,都隱藏著一張張相互關聯的圖數據。這些圖數據彷彿一張張神秘的網,將世界萬物緊密相連。而圖神經網路(GNN)作為一種革命性的技術,正以其強大的能力,逐漸揭開這些圖數據的面紗,讓我們能夠更深入地理解和利用它們。
圖神經網路的出現,為我們提供了一種全新的建模和學習方式。它不僅能夠捕捉資料的空間結構,也能夠揭示圖結構中的複雜關係。無論是在生物學領域,如蛋白質結構分析和藥物發現,或是在社會學領域,如社交網路模擬和輿情分析,圖神經網路都展現了驚人的應用潛力。
更令人興奮的是,圖神經網路還可以與其他機器學習模型進行整合,形成更強大的模型。例如,將圖神經網路與序列模型結合,形成時空圖神經網路(Spatail-Temporal Graph),不僅能夠捕捉資料的時間和空間依賴性,還能夠更全面地揭示資料的內在規律和趨勢。這種融合模式的出現,為各領域的研究和應用帶來了更多的可能性。
在時空圖神經網路中,時間維度被巧妙地引入了圖結構中。這意味著,原本靜止的節點特徵現在會隨著時間的推移而改變。這種變化不僅反映了節點之間的動態關係,還為我們提供了更豐富的訊息,使我們能夠更準確地預測和分析各種複雜現象。
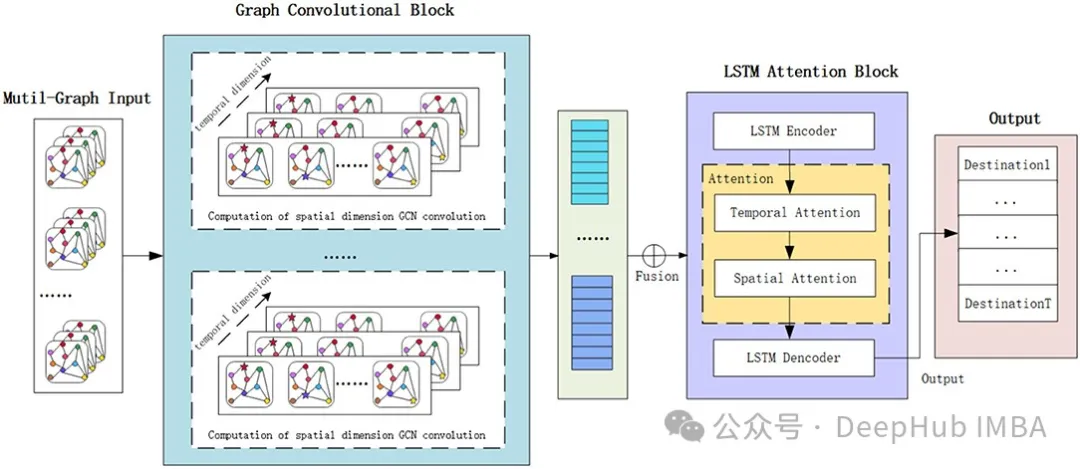
不過,GNN模型和序列模型(如簡單RNN、LSTM或GRU)本身就很複雜。結合這些模型以處理空間和時間依賴性是強大的,但也很複雜:難以理解,也難以實現。
所以在這篇文章中,我們將深入探討這些模型的原理,並實現一個相對簡單的範例,以更深入地理解它們的能力和應用。
圖神經網路(GNN)
我們先介紹一些入門的知識簡單討論GNN。
圖G可以定義為G = (V, E),其中V是節點集,E是它們之間的邊。
包含n個節點的圖的特徵矩陣,每個節點具有f個特徵,是所有特徵的連結:
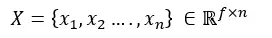
GNN的關鍵問題是所有連接節點之間的訊息傳遞,這種鄰居特徵轉換和聚合可以寫成:

A是圖的鄰接矩陣,I是允許自連接的單位矩陣。雖然這不是完整的方程,但這已經可以說明可以學習不同節點之間空間依賴性的圖卷積網路的基礎。一個經典的圖神經網路如下圖所示:

時空圖神經網路(ST-GNN)
ST-GNN中每個時間步都是一個圖,並透過GCN/GAT網路傳遞,以獲得嵌入資料空間相互依賴性的結果編碼圖。然後這些編碼圖可以像時間序列資料一樣進行建模,只要保留每個時間步驟的資料的圖結構的完整性。下圖示範了這兩個步驟,時間模型可以是從ARIMA或簡單的循環神經網路或是transformers的任何序列模型。

我們下面使用簡單的循環神經網路來繪製ST-GNN的組件
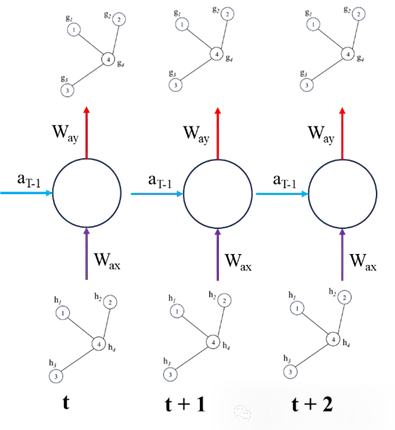
以上就是ST-GNN的基本原理,將GNN和序列模型(如RNN、LSTM、GRU、Transformers 等)結合。如果你已經熟悉這些序列和GNN模型,那麼理論來說是非常簡單的,但是實際操作的時候就會有一些複雜,所以我們下面將直接使用Pytorch實作一個簡單的ST-GNN。
ST-GNN的Pytorch實現
首先要說明:為了用來展示我將使用大型科技公司的股市數據。雖然這些數據本質上不是圖數據,但這種網絡可能會捕捉到這些公司之間的相互依賴性,例如一個公司的表現(好或壞)可能反過來影響市場中其他公司的價值。但這只是一個演示,我們並不建議在股市預測中使用ST-GNN。
載入數據,直接使用yfinance裡面什麼都有
import yfinance as yf
import datetime as dt
import pandas as pd
from sklearn.preprocessing import StandardScaler
import plotly.graph_objs as go
from plotly.offline import iplot
import matplotlib.pyplot as plt
############ Dataset download #################
start_date = dt.datetime(2013,1,1)
end_date = dt.datetime(2024,3,7)
#loading from yahoo finance
google = yf.download("GOOGL",start_date, end_date)
apple = yf.download("AAPL",start_date, end_date)
Microsoft = yf.download("MSFT", start_date, end_date)
Amazon = yf.download("AMZN", start_date, end_date)
meta = yf.download("META", start_date, end_date)
Nvidia = yf.download("NVDA", start_date, end_date)
data = pd.DataFrame({'google': google['Open'],'microsoft': Microsoft['Open'],'amazon': Amazon['Open'],
'Nvidia': Nvidia['Open'],'meta': meta['Open'], 'apple': apple['Open']})
############## Scaling data ######################
scaler = StandardScaler()
data_scaled = pd.DataFrame(scaler.fit_transform(data), columns=data.columns)- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
為了適應ST-GNN,所以我們要將資料轉換以適應模型的要求
將標量時間序列資料集轉換為圖形資料結構是將傳統資料轉換為圖神經網路可以處理的形式的關鍵步驟。這裡描述的功能和類別如下:
- 鄰接矩陣的定義: AdjacencyMatrix 函數定義了圖的鄰接矩陣(連結性),這通常是基於手邊物理系統的結構來完成的。然而,在這裡,作者僅使用了一個全1矩陣,即所有節點都與所有其他節點相連。
- 股市資料集類別: StockMarketDataset 類別旨在為訓練時空圖神經網路(ST-GNNs)建立資料集。這個類別中包含的方法有:
- 資料序列產生: DatasetCreate 方法產生資料序列。
- 建構圖邊: _create_edges方法使用鄰接矩陣建構圖的邊。
- 產生資料序列: _create_sequences方法透過在輸入的股市資料上滑動視窗來產生資料序列。
這種資料準備代碼可以很容易地適應其他問題。這包括定義每個時間步的節點間的連接方式,並利用滑動視窗方法來提取可以供模型學習的序列特徵。透過這種方法,原本簡單的時間序列資料被轉化為具有複雜關係和時間依賴性的圖形資料結構,因此可以使用圖神經網路來進行更深入的分析和預測。
def AdjacencyMatrix(L):
AdjM = np.ones((L,L))
return AdjM
class StockMarketDataset:
def __init__(self, W,N_hist, N_pred):
self.W = W
self.N_hist = N_hist
self.N_pred = N_pred
def DatasetCreate(self):
num_days, self.n_node = data_scaled.shape
n_window = self.N_hist + self.N_pred
edge_index, edge_attr = self._create_edges(self.n_node)
sequences = self._create_sequences(data_scaled, self.n_node, n_window, edge_index, edge_attr)
return sequences
def _create_edges(self, n_node):
edge_index = torch.zeros((2, n_node**2), dtype=torch.long)
edge_attr = torch.zeros((n_node**2, 1))
num_edges = 0
for i in range(n_node):
for j in range(n_node):
if self.W[i, j] != 0:
edge_index[:, num_edges] = torch.tensor([i, j], dtype=torch.long)
edge_attr[num_edges, 0] = self.W[i, j]
num_edges += 1
edge_index = edge_index[:, :num_edges]
edge_attr = edge_attr[:num_edges]
return edge_index, edge_attr
def _create_sequences(self, data, n_node, n_window, edge_index, edge_attr):
sequences = []
num_days, _ = data.shape
for i in range(num_days):
sta = i
end = i+n_window
full_window = np.swapaxes(data[sta:end, :], 0, 1)
g = Data(x=torch.FloatTensor(full_window[:, :self.N_hist]),
y=torch.FloatTensor(full_window[:, self.N_hist:]),
edge_index=edge_index,
num_nodes=n_node)
sequences.append(g)
return sequences- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
訓練-驗證-測試分割。
from torch_geometric.loader import DataLoader
def train_val_test_splits(sequences, splits):
total = len(sequences)
split_train, split_val, split_test = splits
# Calculate split indices
idx_train = int(total * split_train)
idx_val = int(total * (split_train + split_val))
indices = [i for i in range(len(sequences)-100)]
random.shuffle(indices)
train = [sequences[index] for index in indices[:idx_train]]
val = [sequences[index] for index in indices[idx_train:idx_val]]
test = [sequences[index] for index in indices[idx_val:]]
return train, val, test
'''Setting up the hyper paramaters'''
n_nodes = 6
n_hist = 50
n_pred = 10
batch_size = 32
# Adjacency matrix
W = AdjacencyMatrix(n_nodes)
# transorm data into graphical time series
dataset = StockMarketDataset(W, n_hist, n_pred)
sequences = dataset.DatasetCreate()
# train, validation, test split
splits = (0.9, 0.05, 0.05)
train, val, test = train_val_test_splits(sequences, splits)
train_dataloader = DataLoader(train, batch_size=batch_size, shuffle=True, drop_last = True)
val_dataloader = DataLoader(val, batch_size=batch_size, shuffle=True, drop_last=True)
test_dataloader = DataLoader(test, batch_size=batch_size, shuffle=True, drop_last = True)- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
我們的模型包括一個GATConv和2個GRU層作為編碼器,1個GRU層+全連接層作為解碼器。 GATconv是GNN部分,可以捕捉空間依賴性,GRU層可以捕捉資料的時間動態。程式碼包括大量的資料重塑,這樣可以確保每一層的輸入維度相同。這也是我們所說的ST-GNN實作中最複雜的部分,所以如果向具體了解輸各層輸入的維度,可以在向前傳遞的不同階段列印x的形狀,並將其與GRU和Linear層的預期輸入尺寸的文件進行比較。
import torch
import torch.nn.functional as F
from torch_geometric.nn import GATConv
class ST_GNN_Model(torch.nn.Module):
def __init__(self, in_channels, out_channels, n_nodes,gru_hs_l1, gru_hs_l2, heads=1, dropout=0.01):
super(ST_GAT, self).__init__()
self.n_pred = out_channels
self.heads = heads
self.dropout = dropout
self.n_nodes = n_nodes
self.gru_hidden_size_l1 = gru_hs_l1
self.gru_hidden_size_l2 = gru_hs_l2
self.decoder_hidden_size = self.gru_hidden_size_l2
# enconder GRU layers
self.gat = GATConv(in_channels=in_channels, out_channels=in_channels,
heads=heads, dropout=dropout, cnotallow=False)
self.encoder_gru_l1 = torch.nn.GRU(input_size=self.n_nodes,
hidden_size=self.gru_hidden_size_l1, num_layers=1,
bias = True)
self.encoder_gru_l2 = torch.nn.GRU(input_size=self.gru_hidden_size_l1,
hidden_size=self.gru_hidden_size_l2, num_layers = 1,
bias = True)
self.GRU_decoder = torch.nn.GRU(input_size = self.gru_hidden_size_l2, hidden_size = self.decoder_hidden_size,
num_layers =1, bias = True, dropout= self.dropout)
self.prediction_layer = torch.nn.Linear(self.decoder_hidden_size, self.n_nodes*self.n_pred, bias= True)
def forward(self, data, device):
x, edge_index = data.x, data.edge_index
if device == 'cpu':
x = torch.FloatTensor(x)
else:
x = torch.cuda.FloatTensor(x)
x = self.gat(x, edge_index)
x = F.dropout(x, self.dropout, training=self.training)
batch_size = data.num_graphs
n_node = int(data.num_nodes / batch_size)
x = torch.reshape(x, (batch_size, n_node, data.num_features))
x = torch.movedim(x, 2, 0)
encoderl1_outputs, _ = self.encoder_gru_l1(x)
x = F.relu(encoderl1_outputs)
encoderl2_outputs, h2 = self.encoder_gru_l2(x)
x = F.relu(encoderl2_outputs)
x, _ = self.GRU_decoder(x,h2)
x = torch.squeeze(x[-1,:,:])
x = self.prediction_layer(x)
x = torch.reshape(x, (batch_size, self.n_nodes, self.n_pred))
x = torch.reshape(x, (batch_size*self.n_nodes, self.n_pred))
return x- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
訓練過程與pytorch的任何網路訓練過程幾乎相同。
import torch
import torch.optim as optim
# Hyperparameters
gru_hs_l1 = 16
gru_hs_l2 = 16
learning_rate = 1e-3
Epochs = 50
device = 'cuda' if torch.cuda.is_available() else 'cpu'
model = ST_GNN_Model(in_channels=n_hist, out_channels=n_pred, n_nodes=n_nodes, gru_hs_l1=gru_hs_l1, gru_hs_l2 = gru_hs_l2)
pretrained = False
model_path = "ST_GNN_Model.pth"
if pretrained:
model.load_state_dict(torch.load(model_path))
optimizer = optim.Adam(model.parameters(), lr=learning_rate, weight_decay=1e-7)
criterion = torch.nn.MSELoss()
model.to(device)
for epoch in range(Epochs):
model.train()
for _, batch in enumerate(tqdm(train_dataloader, desc=f"Epoch {epoch}")):
batch = batch.to(device)
optimizer.zero_grad()
y_pred = torch.squeeze(model(batch, device))
loss= criterion(y_pred.float(), torch.squeeze(batch.y).float())
loss.backward()
optimizer.step()
print(f"Loss: {loss:.7f}")- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
模型訓練完成了,以下就可以視覺化模型的預測能力。對於每個資料輸入,下面的程式碼預測模型輸出,並隨後繪製模型輸出與基礎真值的關係。
@torch.no_grad()
def Extract_results(model, device, dataloader, type=''):
model.eval()
model.to(device)
n = 0
# Evaluate model on all data
for i, batch in enumerate(dataloader):
batch = batch.to(device)
if batch.x.shape[0] == 1:
pass
else:
with torch.no_grad():
pred = model(batch, device)
truth = batch.y.view(pred.shape)
if i == 0:
y_pred = torch.zeros(len(dataloader), pred.shape[0], pred.shape[1])
y_truth = torch.zeros(len(dataloader), pred.shape[0], pred.shape[1])
y_pred[i, :pred.shape[0], :] = pred
y_truth[i, :pred.shape[0], :] = truth
n += 1
y_pred_flat = torch.reshape(y_pred, (len(dataloader),batch_size,n_nodes,n_pred))
y_truth_flat = torch.reshape(y_truth,(len(dataloader),batch_size,n_nodes,n_pred))
return y_pred_flat, y_truth_flat
def plot_results(predictions,actual, step, node):
predictions = torch.tensor(predictions[:,:,node,step]).squeeze()
actual = torch.tensor(actual[:,:,node,step]).squeeze()
pred_values_float = torch.reshape(predictions,(-1,))
actual_values_float = torch.reshape(actual, (-1,))
scatter_trace = go.Scatter(
x=actual_values_float,
y=pred_values_float,
mode='markers',
marker=dict(
size=10,
opacity=0.5,
color='rgba(255,255,255,0)',
line=dict(
width=2,
color='rgba(152, 0, 0, .8)',
)
),
name='Actual vs Predicted'
)
line_trace = go.Scatter(
x=[min(actual_values_float), max(actual_values_float)],
y=[min(actual_values_float), max(actual_values_float)],
mode='lines',
marker=dict(color='blue'),
name='Perfect Prediction'
)
data = [scatter_trace, line_trace]
layout = dict(
title='Actual vs Predicted Values',
xaxis=dict(title='Actual Values'),
yaxis=dict(title='Predicted Values'),
autosize=False,
width=800,
height=600
)
fig = dict(data=data, layout=layout)
iplot(fig)
y_pred, y_truth = Extract_results(model, device, test_dataloader, 'Test')
plot_results(y_pred, y_truth,9,0) # timestep, node- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
- 61.
- 62.
- 63.
- 64.
對於6個節點(公司),給出過去50個值,做出10個預測。下面是第一個節點的第10步預測與真值的圖。看起來看不錯,但不一定代表就很好。因為對於時間序列數據,下一個值的最佳估計量總是前一個值。如果沒有得到很好的訓練,這些模型可以輸出與輸入資料的最後一個值相似的值,而不是捕捉時間動態。

對於給定的節點,我們可以繪製歷史輸入、預測和真值進行比較,查看預測是否捕捉了模式。
@torch.no_grad()
def forecastModel(model, device, dataloader, node):
model.eval()
model.to(device)
for i, batch in enumerate(dataloader):
batch = batch.to(device)
with torch.no_grad():
pred = model(batch, device)
truth = batch.y.view(pred.shape)
# the shape should [batch_size, nodes, number of predictions]
truth = torch.reshape(truth, [batch_size, n_nodes,n_pred])
pred = torch.reshape(pred, [batch_size, n_nodes,n_pred])
x = batch.x
x = torch.reshape(x, [batch_size, n_nodes,n_hist])
y_pred = torch.squeeze(pred[0, node, :])
y_truth = torch.squeeze(truth[0,node,:])
y_past = torch.squeeze(x[0, node, :])
t_range = [t for t in range(len(y_past))]
break
t_shifted = [t_range[-1]+1+t for t in range(len(y_pred))]
trace1 = go.Scatter(x =t_range, y= y_past, mode = "markers", name = "Historical data")
trace2 = go.Scatter(x=t_shifted, y=y_pred, mode = "markers", name = "pred")
trace3 = go.Scatter(x=t_shifted, y=y_truth, mode = "markers", name = "truth")
layout = go.Layout(title = "forecasting", xaxis=dict(title = 'time'),
yaxis=dict(title = 'y-value'), width = 1000, height = 600)
figure = go.Figure(data = [trace1, trace2, trace3], layout = layout)
iplot(figure)
forecastModel(model, device, test_dataloader, 0)- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.

第一個節點(Google)在測試資料集的4個不同點上的預測其實比我想像的要好,其他的看來不怎麼樣。
總結
我的理解是未來的股票價格不能透過單純的歷史價值自迴歸來預測,因為股票是由現實世界的事件決定的,這並沒有體現在歷史價值中。這也就是我們在前面說的不建議在股市預測中使用ST-GNN,我們使用這個資料集只是因為它容易取得。最後不要忘集我們本篇文章的目的,學習ST-GNN的基本概念,以及透過Pytorch程式碼實作來了解ST-GNN的工作原理。