Retweeted by Terence Tao and led by Fields Medal winners: AI is subverting the way mathematicians work

2024.04.08

Tao Zhexuan liked and retweeted, "Bulletin of the American Mathematical Society" dedicated an entire special issue to introduce the changes brought by AI to mathematics .

These articles are interesting to read, although make one of my own upcoming articles redundant...the field is moving so fast!

The lineup of authors is very luxurious, including Fields Medal winner Akshay Venkatesh , Chinese mathematician Zheng Lejun , computer scientist Ernest Davis and many other well-known scholars.

Among them, Zheng Lejun said that if machines can eventually do better than humans, that would be great, and she would be happy to quit mathematics and play the piano.

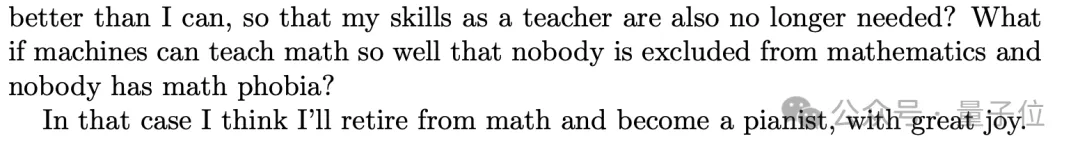
Points they raised included:

AI’s mathematical capabilities do not fully reflect human cognitive processes and rely on patterns in training data rather than truly understanding the nature of the problem.
Synthetic mathematics , such as synthetic topology and synthetic differential geometry, provides a new way of practicing mathematics, allowing mathematicians to focus on deeper concepts and problems.
Interactive proof systems and "norm-driven development" in software engineering can reduce mathematicians' cognitive load and promote collaboration among mathematicians.
Formal proof technology may change the nature of mathematical proof and subvert the way mathematicians work.
The mathematics community should not be hijacked by the agenda dominated by technology companies.

In the opening chapter, the editorial board wrote:

Pure mathematicians are used to enjoying a large degree of research autonomy and intellectual freedom, a fragile and precious legacy that can be swept away by the mindless use of machines.

On the other hand, a thoughtful and considered approach to the same technology could greatly enrich our discipline.

It is up to us to decide how the discipline should develop, so we invite the mathematics community to think carefully about and discuss the questions raised in the special issue, and to listen to colleagues in other fields think deeply about these issues.

Now is the time for mathematicians to understand and contribute to this debate and determine the future direction of the discipline.

Can AI automatically prove theorems?

Computers have played an important role in mathematics, especially in improving computational efficiency, but can they help humans perform mathematical reasoning? Will they one day reason on their own?

Mathematician Kevin Buzzard provides an overview of recent developments in neural networks, computer theorem provers, and large language models.

Kevin Buzzard is currently a professor of mathematics at Imperial College London, UK. He specializes in arithmetic geometry and the Langlands Program.

Looking back at the entire history of computing tools, the earliest word computer also referred to human beings as "calculators", and their achievements should not be underestimated.

In the early 17th century, Scottish mathematician John Napier constructed the first logarithm table, and he suggested that the work could be further advanced if more "calculators" came to help.

Another representative result was the integer factorization table published by Felkel and Vega in the 1770s, which made it possible to study the distribution of prime numbers and eventually led to the proof of the prime number theorem.

After the emergence of early electronic computers, machines have far surpassed humans in high-speed calculations, and the meaning of the word Computer has also changed.

For example, the University of Cambridge purchased the EDSAC II computer in 1957 for oceanographic calculations, laying the foundation for modern plate tectonics theory.

At this stage, the computer is just a tool. Even current computers are difficult to perform mathematical reasoning and theorem proving like humans.

Neural networks can be used to search for theorems, guess new theorems, and find counterexamples. For example, new theorems about the relationship between nodes and edges in topology were discovered, and new results about Kazhdan-Lusztig polynomials were discovered in representation theory, but for There are limitations to proving esoteric and complex theorems.

The Automatic Theorem Proving System (ATP) can automatically prove some complex theorems, such as Robbins' conjecture. But the proofs generated by ATP are often too lengthy and difficult for humans to understand.

The Interactive Theorem Proving System ( ITP) can be used to verify the correctness of theorems and help discover and correct errors in mathematical literature. For example, mathematician Peter Scholze admitted in the Liquid Tensor Experiment that he could not master all involved Mathematical objects and concepts are finally completed with the help of the Lean system.

Although large models such as ChatGPT can generate relevant mathematical content, they are prone to errors. Buzzard recommends that large models be used in conjunction with systems such as ITP to increase reliability by generating preliminary proofs through large models that are then verified by ITP.

Buzzard believes that these emerging technologies can help mathematicians break through cognitive barriers, explore more complex and novel mathematical fields , and ultimately change the way mathematicians work, allowing them to devote more time and energy to mathematical thinking and understanding. .

The other three articles explore from different perspectives how these emerging technologies can help mathematicians cope with increasing complexity and open up new areas of mathematics.

The formal turn in mathematics

Logician Jeremy Avigad discusses how, since the early 20th century, mathematical definitions and proofs can be expressed in formal systems with precise syntax and usage rules.

Jeremy Avigad is a professor of philosophy and mathematics at Carnegie Mellon University, where he has made contributions in the fields of mathematical logic and foundations, formal verification and interactive theorem proving, and mathematical philosophy and history.

He believes that this shift may change the nature of mathematics, and proofs that rely on machine verification may reduce mathematicians' emphasis on intuitive understanding and insight, which may affect the process of mathematical discovery and the development of mathematical ideas.

Abstract Boundaries and Specification-Driven Development in Pure Mathematics

Mathematicians Johan Commelin and Adam Topaz explore how abstraction boundaries , with the help of interactive theorem provers, can help control complexity in mathematical research.

Johan Commelin is an assistant professor at Utrecht University in the Netherlands, and Adam Topaz is an assistant professor at the University of Alberta. The intersection of their research interests is algebraic geometry, and they jointly participated in liquid tensor experiments.

△左：Johan Commelin，右：Adam Topaz

The abstract boundary refers to the boundary that formally distinguishes the implementation details of mathematical objects from their external properties and behaviors in the process of mathematical research and theorem proving. This bound allows mathematicians to use and reason about these mathematical objects without relying on specific implementation details.

The concept of abstract boundaries is very common in software engineering, for example, implemented through header files in C language, public methods in object-oriented programming, or typeclasses in functional programming.

A "specification-driven development" approach based on abstract boundaries not only reduces cognitive load, but also facilitates collaboration among mathematicians, allowing work to be easily distributed among collaborators with different expertise.

Strange New Worlds: Theorem Proving Assistants and Composition Basics

Mathematician Michael Shulman believes that existing computer programs such as Lean Proof Assistant can verify the correctness of mathematical proofs, but their specialized proof languages are a threshold for many mathematicians.

Michael Shulman is an associate professor at the University of San Diego. His research fields are category theory and algebraic topology.

Existing computer proof assistants can verify the correctness of mathematical proofs, but their specialized proof languages are a barrier to entry for many mathematicians. Large models have the potential to lower this barrier, allowing mathematicians to interact with proof assistants in a more familiar language.

This could allow mathematicians to explore fundamentally new areas of mathematics using model-supported proof assistants, a role that existing proof assistants already fulfill in areas such as homotopy type theory .

Can current artificial intelligence do serious math?

Ernest Davis , a computer scientist at New York University, pointed out that current AI cannot reliably combine basic mathematics and common sense reasoning when solving mathematical problems described in words.

There are three main ways in which AI attempts to solve mathematical problems, but each method has its advantages and limitations.

Directly generate answers , suitable for simple math problems.
Generating executable code has been successful in practice.
Translated into logical specifications , there are still challenges for complex problems.

他认为AI在解决数学奥林匹克问题时可能会依赖于训练数据中的模式，而不是真正理解问题的本质，这与人类通过直观和逻辑推理解决问题的方式有显著差异。

AI needs three types of knowledge to truly solve mathematical problems: basic mathematics, language understanding, and world knowledge . Such as understanding the value and physical properties of coins. Common sense is often overlooked when solving problems, but is actually crucial.

Benchmark test sets are an important tool for evaluating the performance of AI systems, but they may not comprehensively cover all capabilities of AI.

But at the same time, he also pointed out that although AI has limitations in dealing with basic problems, this may not affect its ability to conduct advanced mathematical research .

On the one hand, advanced mathematical studies may not require the same common sense reasoning skills as solving basic problems.

On the other hand, in chess games, even if AI cannot understand the basic concepts of the chess game, its ability to analyze the chess game and formulate strategies can far exceed that of human chess players.

What do mathematicians think of AI?

Some thoughts on automation and mathematical research

Fields Medalist Akshay Venkatesh discusses the impact of mathematical automation on mathematical research. He pointed out that machines may greatly enhance the ability of mathematics to solve problems, but they will also completely change the core problems and values of mathematics, making it difficult for humans to understand.

He analyzed that the current mechanisms by which the mathematics community determines "what is important" , such as journals, awards, recognition of mathematical theories in applied fields, education systems, hiring and funding processes, etc., are not sufficient to explain the relatively high level of consensus in the mathematics community.

He sees it as “proven” that this particular form of academic communication elicits consensus, similar to the mechanisms by which information spreads in the free market.

AI will lead to drastic changes in the current judgment of "importance" in the mathematics community.

How machines can make math more inclusive

Mathematician Eugenia Cheng believes that technology is already changing the way people study mathematics, and these technologies can be used to make mathematics more inclusive rather than making mathematicians redundant.

Lejun Zheng teaches at the University of Sheffield. In addition to category theory research and undergraduate teaching, her goal is to eliminate "mathematics phobia" in the world.

She analyzes how technology impacts mathematics teaching, problem-raising, collaboration, dissemination, and research:

Teaching: Standard “chalk and blackboard” lectures became unnecessary and she began to adopt a more interactive teaching style. At the same time, for students, memory is now irrelevant and their brains should be left to more interesting things.
Asking questions: Technology allows anyone to ask questions online and get answers, but it has inherited and amplified the elitism and competitiveness of the math community.
Collaboration: Technology has greatly facilitated remote collaboration, making geographical location no longer a barrier. Tools such as electronic whiteboards also greatly enhance the convenience of collaboration.
Dissemination: The Internet has made dissemination of papers popular and is no longer limited to limited paper journals. This makes the paper publishing process more open and transparent, and the quality of the paper rather than the publication channel becomes the key.
Research: Use your smartphone to conduct research anytime, anywhere, regardless of location. Search engines and the like also save her from having to remember all the facts and can look them up at any time.

In general, Lejun Zheng believes that technology can make mathematics more inclusive, as long as mathematicians make good use of these technologies instead of resting on their laurels.

At the same time, she also proposed that if machines can eventually do better than humans, that would be great, and she would be happy to quit mathematics and play the piano .

Proof in the machine age

Number theorist Andrew Granville focuses on the nature of proof and the relationship between computer proof and human proof.

He believes that "objectivity" in pure mathematics is not as unbreakable as we think.

Difficulties in definitions and concepts: Many concepts in modern mathematics do not have a single clear definition, and there are many possible definitions and interpretations. This makes it difficult to talk about "objectivity".
Limitations of the axiomatic system: According to Gödel's incompleteness theorem, even with a consistent axiomatic system, it is impossible to prove all correct statements about integers. This shows that "objective" mathematical foundations have limitations.
The influence of historical evolution: Mathematicians in different eras have different understandings and standards of "mathematical proof", which reflects the changes in objectivity standards.

He discusses the challenges and opportunities that automated computer proofs may present. Computer proofs can help confirm the correctness of human intuitive proofs and improve credibility. But computer proofs may replace humans and become "black box" proofs. But this proof may lack the comprehensibility and adaptability that humans should have.

Granville hopes that future computer proofs can absorb the advantages of human proofs and maintain sufficient flexibility and understandability on a formal basis.

Automation forces mathematicians to rethink their values

Columbia University mathematician Michael Harris emphasized that mathematics needs to absorb the experience of other disciplines, especially the humanities and social sciences.

He suggested that frequent reflection on the value pursuit and material foundation of the discipline would help mathematicians better defend the core values of mathematics when facing challenges such as automation.

In addition, he also warned that the mathematics community should not be kidnapped by the agenda dominated by technology companies . The value orientation of technology companies is not completely consistent with that of mathematicians. Mathematicians should maintain the courage to think independently instead of passively accepting advice from industry. Value orientation.

新聞