DifFlow3D：場景流估計新SOTA，擴散模型又下一城

論文想法：

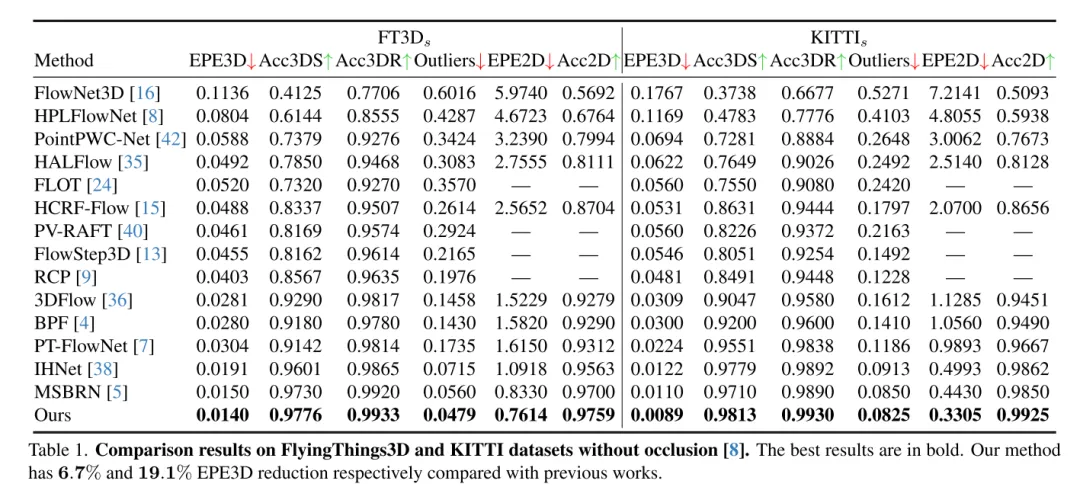
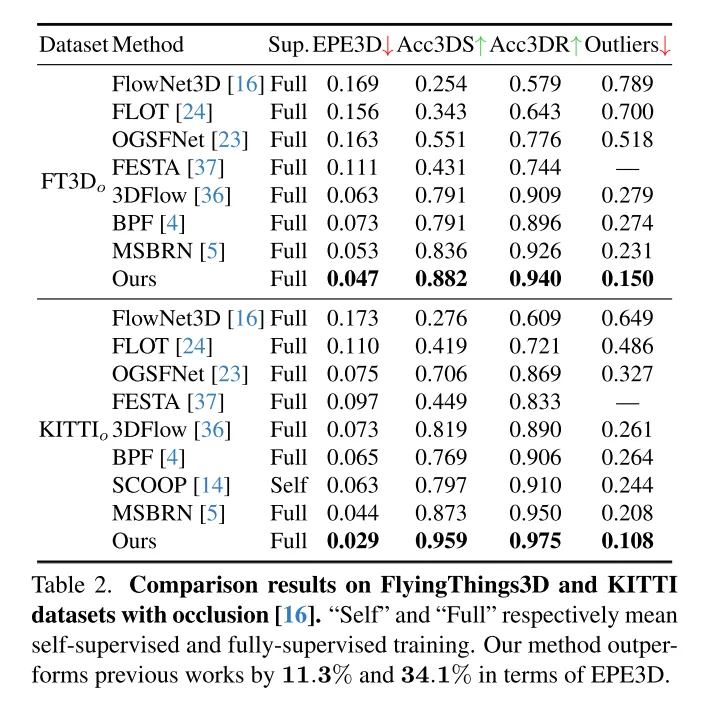
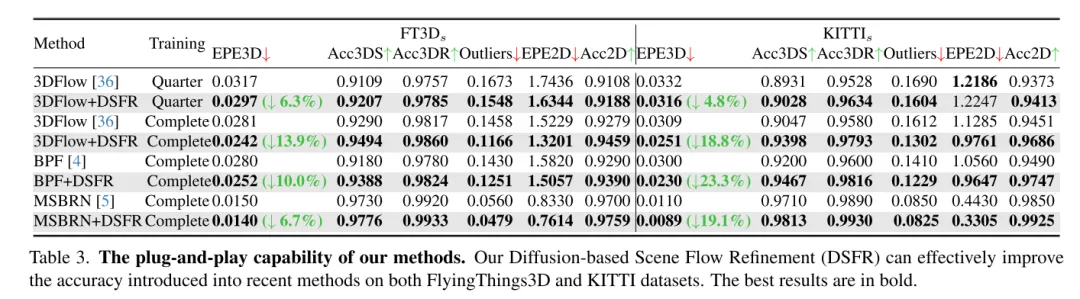
場景流估計旨在預測動態場景中每個點的3D位移變化，是電腦視覺領域的基礎任務。然而，以往的工作常常受到局部約束搜尋範圍引起的不可靠相關性的困擾，並且在從粗到細的結構中累積不準確性。為了緩解這些問題，本文提出了一種新穎的不確定性感知場景流估計網路（DifFlow3D），該網路採用了擴散機率模型。設計了迭代擴散式細化(Iterative diffusion-based refinement)來增強相關性的穩健性，並對困難情況（例如動態、雜訊輸入、重複模式等）具有較強的適應性。為了限制生成的多樣性，本文的擴散模型中利用了三個關鍵的與流相關的特徵作為條件。此外，本文還在擴散中開發了一個不確定性估計模組，以評估估計場景流的可靠性。本文的DifFlow3D 在FlyingThings3D 和KITTI 2015 資料集上分別實現了6.7%和19.1%的三維端點誤差（EPE3D）降低，並在KITTI資料集上實現了前所未有的毫米級精度（EPE3D為0.0089米）。另外，本文的基於擴散的細化範式可以作為一個即插即用的模組，輕鬆整合到現有的場景流網路中，顯著提高它們的估計精度。

主要貢獻：

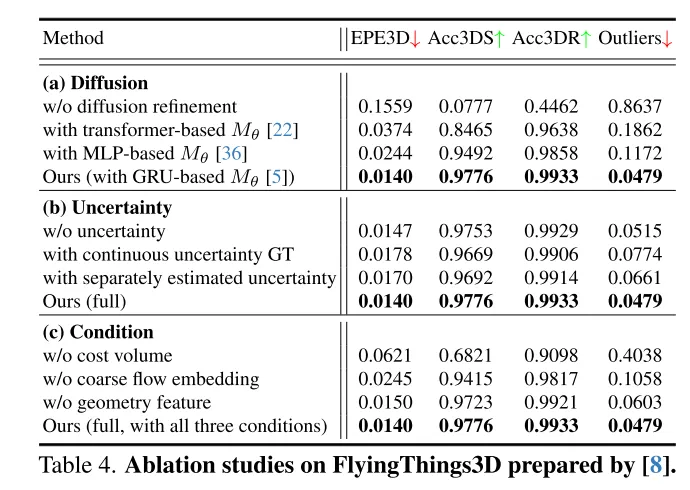
為了實現穩健的場景流估計，本文提出了一種新穎的即插即用型基於擴散的細化流程。據本文所知，這是首次在場景流任務中利用擴散機率模型。

本文透過結合粗流嵌入、幾何編碼和跨幀成本體積(coarse flow embeddings, geometry encoding, cross-frame cost volume)，設計了強有力的條件引導來控制生成的多樣性。

為了評估本文估計流的可靠性並識別不準確的點匹配，本文還在本文的擴散模型中引入了每個點的不確定性估計。

本文的方法在FlyingThings3D 和KITTI 資料集上均優於所有現有方法。特別是，本文的DifFlow3D 首次在KITTI 資料集上實現了毫米級的端點誤差（EPE3D）。與以往的工作相比，本文的方法對於具有挑戰性的情況具有更強的穩健性，例如雜訊輸入、動態變化等。

網路設計：

場景流作為電腦視覺中的一項基礎任務，指的是從連續的影像或點雲中估計出的三維運動場。它為動態場景的低層次感知提供了訊息，並且有著各種下游應用，例如自動駕駛[21]、姿態估計[9]和運動分割[1]。早期的工作集中在使用立體[12]或RGB-D影像[10]作為輸入。隨著3D感測器，例如光達的日益普及，近期的工作通常直接以點雲作為輸入。

作為開創性的工作，FlowNet3D[16]使用PointNet++[25] 提取層次化特徵，然後迭代回歸場景流。PointPWC[42] 透過金字塔、變形和成本體積結構[31]進一步改進了它。HALFlow[35] 跟隨它們，並引入了注意力機制以獲得更好的流嵌入。然而，這些基於迴歸的工作通常遭受不可靠的相關性和局部最優問題[17]。原因主要有兩個面向：（1）在他們的網路中，使用K最近鄰（KNN）來搜尋點對應關係，這並不能考慮到正確但距離較遠的點對，也存在著匹配雜訊[7] 。（2）另一個潛在問題來自於以往工作[16, 35, 36, 42]中廣泛使用的粗到細結構。基本上，最初的流在最粗糙的層上估計，然後在更高分辨率中迭代細化。然而，流細化的性能高度依賴於初始粗流的可靠性，因為後續的細化通常受限於初始化周圍的小的空間範圍。

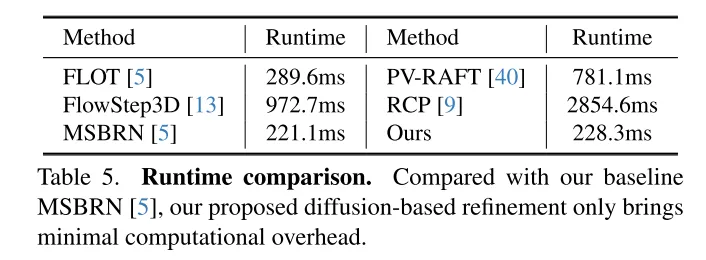
為了解決不可靠性的問題，3DFlow[36] 設計了一個all-to-all 的點收集模組，並加入了反向驗證。類似地，Bi-PointFlowNet[4] 及其擴展MSBRN[5] 提出了一個雙向網絡，具有前向-後向相關性。IHNet[38] 利用一個具有高解析度引導和重採樣方案的循環網路。然而，這些網路大多因其雙向關聯或循環迭代而在計算成本上遇到了困難。本文發現擴散模型也可以增強相關性的可靠性和對匹配雜訊的韌性，這得益於其去噪本質（如圖1所示）。受到[30]中的發現的啟發，即註入隨機噪聲有助於跳出局部最優，本文用概率擴散模型重新構建了確定性流回歸任務(deterministic flow regression task)，如圖2所示。此外，本文的方法可以作為一個即插即用的模組服務於先前的場景流網絡，這種方法更為通用，並且幾乎不增加計算成本（第4.5節）。

然而，在本文的任務中利用生成模型是相當具有挑戰性的，因為擴散模型固有的生成多樣性。與需要多樣化輸出樣本的點雲產生任務不同，場景流預測是一個確定性任務，它計算精確的每點運動向量。為了解決這個問題，本文利用強條件資訊來限制多樣性，並有效控制生成的流。具體來說，先初始化一個粗糙的稀疏場景流，然後透過擴散迭代產生流殘差(flow residuals)。在每個基於擴散的細化層中，本文利用粗流嵌入、成本體積和幾何編碼作為條件。在這種情況下，擴散被應用於實際學習從條件輸入到流殘差的機率映射。

此外，先前的工作很少探索場景流估計的置信度和可靠性。然而，如圖1所示，在雜訊、動態變化、小物體和重複模式的情況下，密集流匹配容易出錯。因此，了解每個估計的點對應關係是否可靠是非常重要的。受到最近在光流任務中不確定性估計成功的啟發[33]，本文在擴散模型中提出了逐點不確定性，以評估本文的場景流估計的可靠性。

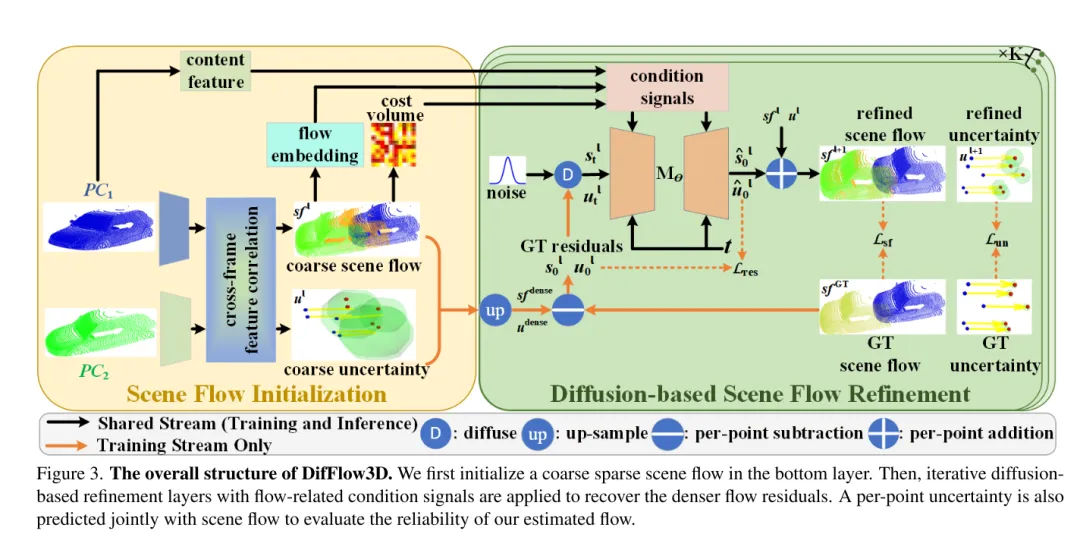
圖3。DifFlow3D 的整體結構。本文首先在bottom layer 初始化一個粗糙的稀疏場景流。隨後，將迭代擴散式細化層與流相關的條件訊號結合使用，以恢復更密集的流殘差。為了評估本文估計的流的可靠性，也將與場景流一起共同預測每個點的不確定性。

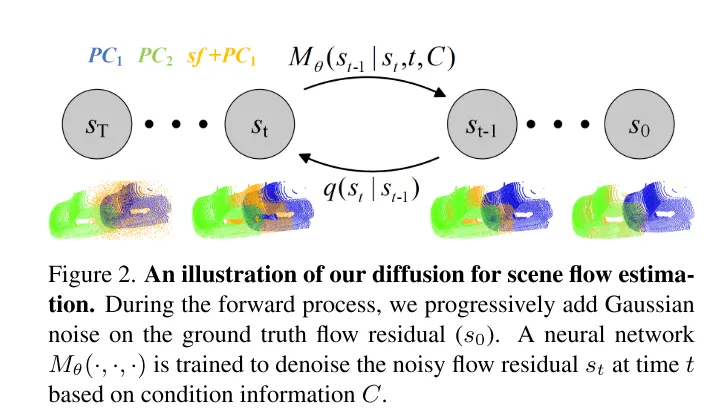
圖2。本文用於場景流估計的擴散過程示意圖。

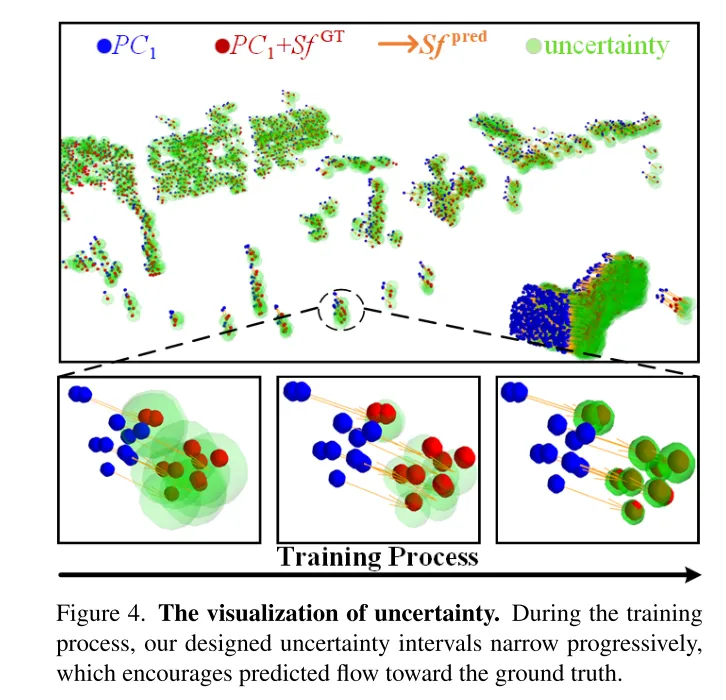
圖4。不確定性的可視化。在訓練過程中，本文設計的不確定性區間逐漸縮小，促使預測的流向真實值靠攏。

實驗結果：

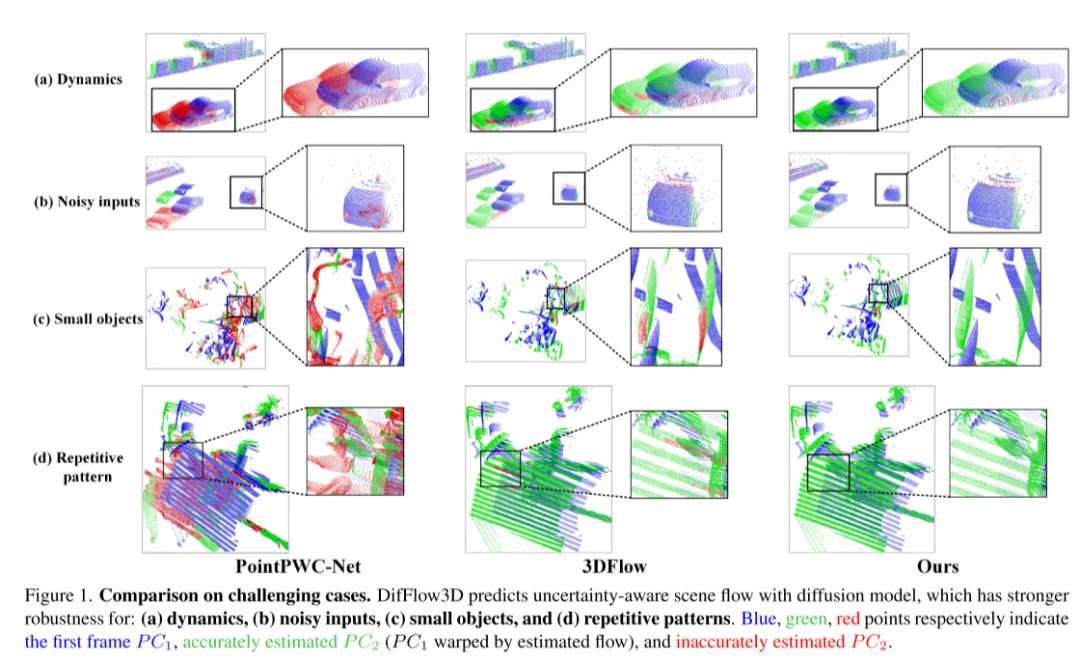
圖1。在具有挑戰性的情況下的比較。DifFlow3D 使用擴散模型預測具有不確定性感知的場景流，該模型對以下情況具有更強的魯棒性：(a)動態變化，(b)噪聲幹擾的輸入，(c)小物體，以及(d )重複模式。

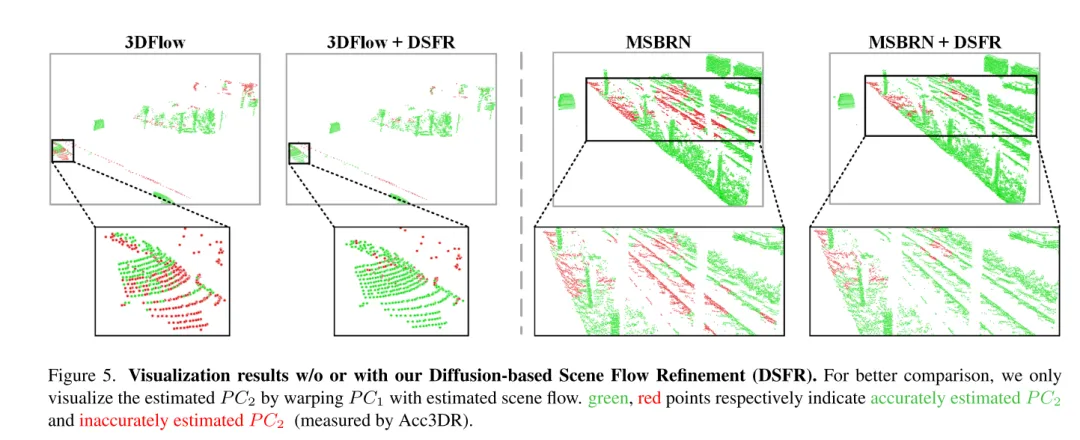
圖5. 未使用或使用基於擴散的場景流細化(DSFR) 的可視化結果。

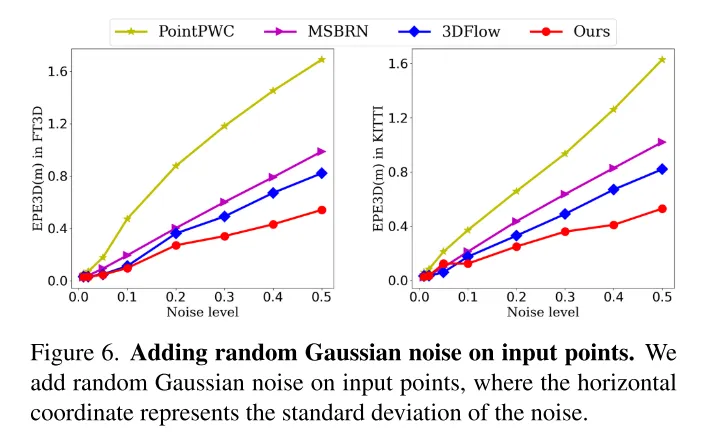
圖6。在輸入點上加入隨機高斯雜訊。

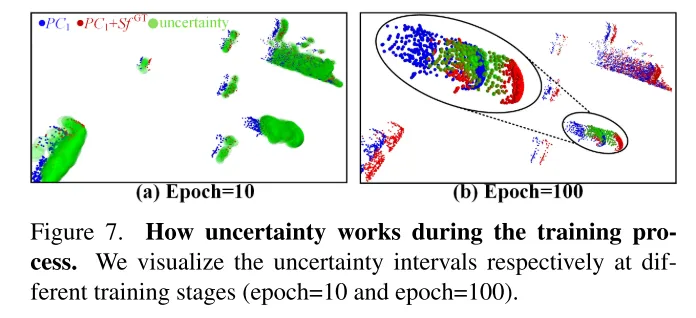
圖7。不確定性在訓練過程中的作用。本文分別在不同的訓練階段（第10輪和第100輪）可視化了不確定性區間。

總結：

本文創新地提出了一個基於擴散的場景流細化網絡，該網絡能夠感知估計的不確定性。本文採用多尺度擴散細化來產生細粒度的密集流殘差。為了提高估計的穩健性，本文也引入了與場景流一起聯合生成的逐點不確定性。廣泛的實驗顯示了本文的DifFlow3D 的優越性和泛化能力。值得注意的是，本文的基於擴散的細化可以作為即插即用模組應用於以往的工作，並為未來的研究提供新的啟示。