Logic programming: ancient artificial intelligence language Prolog

Today I would like to introduce you to an interesting programming language.

It allows the computer to reason like a detective and think like a philosopher. This is logic programming.

Logic programming is like giving the computer a logic puzzle, and then it finds the answer through a series of reasoning.

1 What is logic programming?

1.1 Definition and characteristics of logic programming

Imagine what it would be like if we could make computers think and solve problems like humans. Logic programming is an attempt to use the principles of logic to enable computers to reason and solve problems.

We just need to tell the computer: "This is the rule, this is the fact, now you tell me the answer." It's like playing a game of serial reasoning, each clue gradually reveals part of the puzzle, and finally reveals the entire story.

Logic programming is characterized by a high degree of abstraction, not focusing on how to operate, but focusing on "what is true".

1.2 Representative language: Prolog

Prolog, or Programming in Logic, is a representative language for logic programming. At its core are facts and rules. Let’s take a look at the basic syntax of Prolog:

• Facts: In Prolog, we can define some basic facts. For example, philosopher(socrates). means "Socrates is a philosopher".
• Rules: Rules are used to define relationships between facts. For example, mortal(X) :- philosopher(X). means "If someone is a philosopher, then he must be a mortal". X represents parameters, capital letters are variables and lowercase letters are constants. Symbol:- represents an inference relationship. If the expression on the right is true, the expression on the left is also true.
• Query: A query is a question posed to a Prolog program. For example, ?-mortal(socrates). would ask "Is Socrates mortal?". ?- is the command prompt. We enter the command to be executed at the end and press Enter to execute it and return the result.

Note that all statements end with a dot (.) to indicate the end.

The charm of Prolog lies in its simplicity and power. We don't need to tell the computer how to solve the problem step by step, we just need to tell it the rules and facts, and it can automatically perform logical reasoning and finally give us the answer.

2 Application areas of logic programming

2.1 Expert system

Expert system is a major application of logic programming, which is like having a team of expert consultants. They can help doctors diagnose disease or help engineers design complex mechanical structures. Taking medical diagnosis as an example, in Prolog, we can define a series of relationships between symptoms and diseases. For example:

disease(flu) :- symptom(fever), symptom(cough).
1.

This rule tells the computer: "If a person has symptoms of fever and cough, then he may have the flu." Through such rules, expert systems can help doctors diagnose diseases.

2.2 Natural language understanding

Natural language understanding allows computers to understand human language. It's like putting a pair of glasses on the computer that understands human language. It can read your emails and understand your instructions. For example, we can use Prolog to parse the structure of a sentence:

sentence(Subject, Verb, Object) :- noun(Subject), verb(Verb), noun(Object).
1.

This rule can help computers understand the sentence structure of "subject + predicate + object". In this way, the computer can better understand the user's input.

2.3 Intelligent knowledge base

An intelligent knowledge base is like a huge electronic brain that stores massive amounts of information. Logic programming allows this brain to think and reason on its own, helping us find the knowledge we need. For example, a knowledge base about historical figures might contain rules such as:

born_in(bruce_lee, san_francisco).
performed(bruce_lee, the_game_of_death).
1.
2.

Through such facts and rules, users can query Bruce Lee's birthplace and which movies he has participated in.

3 How does logic programming solve problems?

3.1 Build the model

The first step in solving a problem is to build a model. Just like building a bridge, we need to define the structure and support points of the bridge. In logic programming, we define rules or constraints, such as: "Philosophers are human."

mortal(X) :- philosopher(X).
1.

3.2 Define rules and facts

Next, we add rules and facts to the model. If the model is the structure of the bridge, then the rules and facts are like the vehicles running on the bridge. For example, we state: "Socrates, Plato, and Aristotle were philosophers."

philosopher(socrates).
philosopher(plato).
philosopher(aristotle).
1.
2.
3.

3.3 Derivation and solution

Finally, we ask questions, such as: "Who is a mortal?" Logic programming is like a smart little detective. It will automatically deduce logic and find out all possible answers, such as output: "Socrates, Plato, Aris Dodd."

There are many implementations of Prolog. This article uses the currently active SWI-Prolog as an example to run this program.

You need to first save the rules and facts to a file mortal.pl, then use the command consult to load the rules, and finally execute mortal(X). To get the results, when there are multiple answers, we enter a semicolon (;) and Prolog will continue to search. Until all possible answers have been found.

picture

SWI-Prolog official website: https://www.swi-prolog.org/

Executable program: https://www.swi-prolog.org/download/stable

Docker image: https://hub.docker.com/_/swipl/

Source code: https://github.com/SWI-Prolog/swipl-devel

4 Common problems and solutions in logic programming

4.1 Map coloring problem

Imagine you have a map and you need to color each area with a different color, but adjacent areas cannot be the same color.

(Source of pictures and solution methods: https://ruanyifeng.com/blog/2019/01/prolog.html)

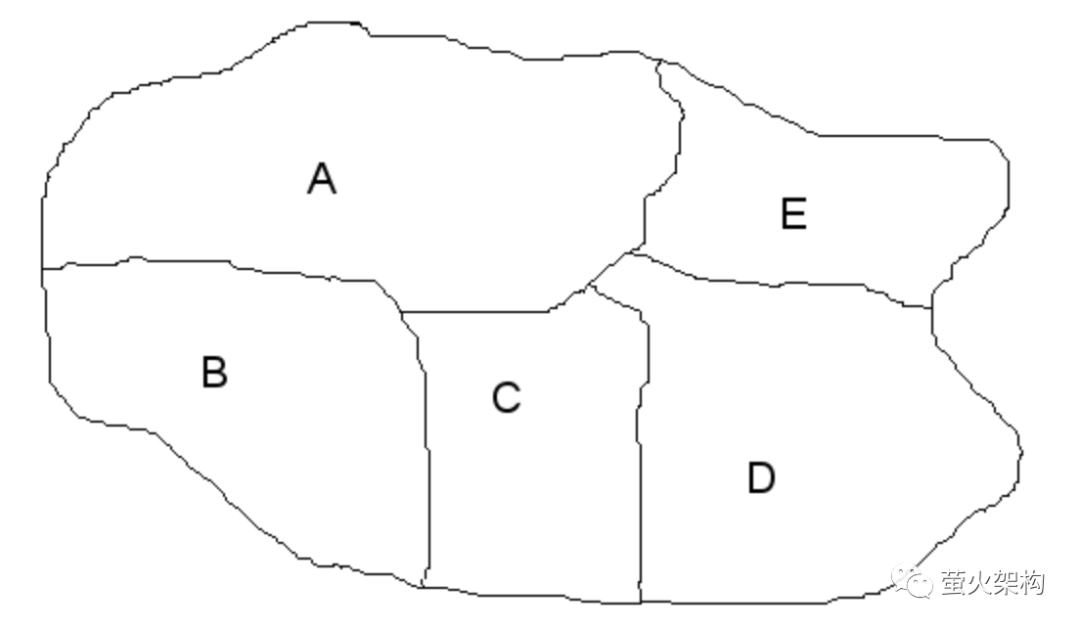picture

The rules are as follows:

color(red).
color(green).
color(blue).

color_solution(A,B,C,D,E) :-
    color(A), color(B), color(C), color(D), color(E),
    \+ A=B, \+ A=C, \+ A=D, \+ A=E,
    \+ B=C, \+ C=D, \+ D=E.
1.
2.
3.
4.
5.
6.
7.
8.

If there are multiple conditions on the right, separate them with commas; if you want to use a negative expression, add \+ before the expression.

The calculation speed is still relatively fast, and the execution effect is as follows:

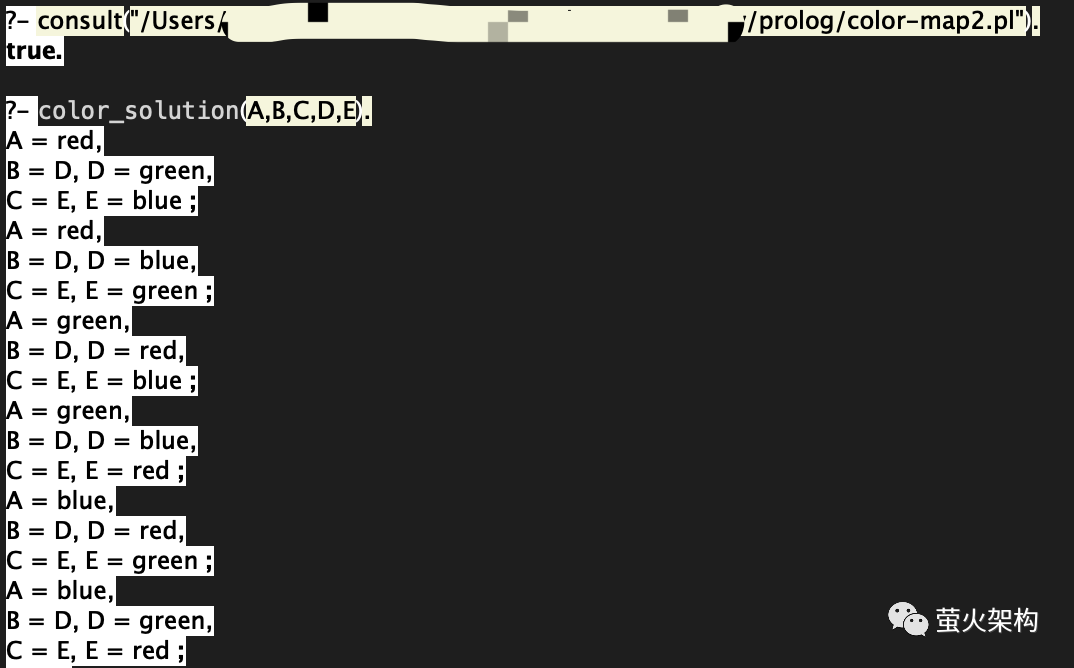picture

4.2 Questions about suspect’s reasoning

When a detective solves a case, he needs to consider all suspect motives and evidence. Logic programming can help detectives sort through this information and deduce the real culprit.

Assume the rules are as follows:

% 犯罪嫌疑人
suspect(zhangsan).
suspect(lisi).
suspect(wangwu).

% 犯罪发生在夜晚
crime_occurred(night).

% 无辜的
innocent(Person) :- suspect(Person), not_at_scene(Person, Time), crime_occurred(Time).

% 假设我们知道Alice和Charlie在犯罪发生时有不在场证明
not_at_scene(zhangsan, night).
not_at_scene(lisi, night).
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.

We can figure out who is innocent and who cannot be ruled out of suspicion according to the rules and facts. The demonstration effect is as follows:

picture

4.3 Find the approximate optimal solution

Sometimes, the problem may not have a perfect solution, and the cost of finding the optimal solution is very high. We can just find an approximate solution. Let’s take the Knapsack Problem as an example. In this problem, we need to pack as many items with the largest total value as possible without exceeding the weight limit of the knapsack.

Suppose we have a list of items, each with a weight and value, and a maximum weight limit for a backpack. This code is relatively complex, and there are better solutions. If you are interested, you can study it.

% 物品列表：item(物品ID, 价值, 重量).
item(1, 15, 20).
item(2, 20, 30).
item(3, 15, 25).
item(4, 22, 25).

% 背包最大重量限制
max_weight(50).

% 检查物品组合是否超过最大重量
within_weight_limit(Items, MaxWeight) :-
    total_weight(Items, TotalWeight), %通过调用total_weight计算物品重量
    TotalWeight =< MaxWeight.

% 计算物品组合的总重量，这里是一个递归规则。
% 它分两种情况：一个是空列表的总重量为0，另一个是包含至少一个物品的列表。
% 对于非空列表，它计算列表头部物品的重量，然后递归地计算列表剩余部分的总重量，最后将两者相加。
total_weight([], 0).
total_weight([Item|Rest], TotalWeight) :-
    item(Item, _, ItemWeight),
    total_weight(Rest, RestWeight),
    TotalWeight is ItemWeight + RestWeight.

% 计算物品组合的总价值，这也是一个递归规则
total_value([], 0).
total_value([Item|Rest], TotalValue) :-
    item(Item, ItemValue, _),
    total_value(Rest, RestValue),
    TotalValue is ItemValue + RestValue.

% 暴力搜索所有的组合，可以看作是一种深度优先搜索
% max_weight把背包的最大容量取出来
% findall是Prolog内置的，把所有物品的Id取出来
% subset把所有物品的组合取出来，定义见下方，结果将被绑定到变量Solution
% within_weight_limit 判断方案是否在重量限制中
% 如果Solution的总重量在限制范围内，这个调用会计算其总价值并将其绑定到变量Value。
iterative_deepening_knapsack(Solution, Value) :-
    max_weight(MaxWeight),
    findall(Item, item(Item, _, _), AllItems),
    subset(AllItems, Solution),
    within_weight_limit(Solution, MaxWeight),
    total_value(Solution, Value).

% 用于查找所有可能组合（子集），这也是一个递归定义
% 空列表是其自身的子集。
% 如果列表的头部是E，并且Tail的一个子集是NTail，那么添加E到NTail的头部形成的列表也是原始列表的一个子集。这条规则包含列表中的第一个元素。
% 无论列表的头部是什么（这里用匿名变量_表示），Tail的一个子集NTail也是原始列表的一个子集。这条规则不包含列表中的第一个元素。
subset([], []). 
subset([E|Tail], [E|NTail]):- subset(Tail, NTail).
subset([_|Tail], NTail):- subset(Tail, NTail).

% 寻找近似最优解
% 使用findall运行iterative_deepening_knapsack 来收集所有解决方案的价值
% 使用max_list找到最高的价值
% 再次运行iterative_deepening_knapsack来找到与最高价值对应的物品组合
% 返回最高价值ApproxValue和对应的物品组合ApproxItems作为查询结。
approximate_solution(ApproxValue, ApproxItems) :-
    findall(Value, iterative_deepening_knapsack(_, Value), Values),
    max_list(Values, ApproxValue),
    iterative_deepening_knapsack(ApproxItems, ApproxValue).
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
twenty one.
twenty two.
twenty three.
twenty four.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.

The actual operating effect is as follows:

picture

Conclusion

Logic programming languages ​​have a long history and are usually used in education, research and certain professional application fields, such as artificial intelligence, knowledge representation, natural language processing, expert systems, etc. However, we rarely use them daily, mainly because its performance is not very good. Good, and the learning curve is relatively steep, and the industry’s acceptance is not very high.

However, in artificial intelligence, its ability to represent knowledge and reasoning is still good. In the future, it may be more combined with imperative and functional programming paradigms to provide more powerful and flexible programming tools.

Finally, logic programming is like giving the computer a thinking ability. Those who are interested can learn it together.