Part 01. Introduction to Community Discovery 

A complex network is a network structure formed by a large number of network nodes and intricate link relationships between nodes. Many natural, scientific, social relations and infrastructure systems encountered in life can be represented by complex network modeling, such as power systems, social networks, communication networks, transportation networks, etc. Expressed in the language of mathematics, a complex network is a graph with sufficiently complex topological features.

Figure 1 Various complex networks connect people and people, people and things in modern society

Complex networks can always be further divided into various communities. The so-called community is a special subgraph structure in the network, which is shown in the topological structure: the members of the community are closely connected, but the connection with the rest of the network is relatively sparse. Community discovery algorithm can be used to reveal community structure in complex networks, and it is a novel tool that can analyze networks from a micro perspective. Therefore, community discovery algorithms are currently widely used in various Internet companies to assist researchers in understanding information in complex networks, and can be seen in social network analysis, recommendation systems, risk control and other fields. Whether it is Douyin user risk control based on social network data, QQ/Weibo friend recommendation, or urban traffic flow prediction and power grid load analysis based on real-world data, these applications are inseparable from the drive of community discovery algorithms.

Part 02. Common community discovery techniques

Community detection is a rich and challenging problem, partly because the definition of a community remains poorly described. In graph theory, a community is defined as a non-overlapping group of nodes with far more edge connections within the group than between groups. But this definition still leaves many possibilities, and correspondingly many calculation methods based on theories in different fields have been proposed.

- Optimization-based approach

The most common method is based on optimization, greedy algorithm, simulated annealing algorithm, Louvain algorithm, PSO algorithm, evolutionary multi-objective optimization algorithm, etc. all belong to this category. A typical optimization method first needs to establish a community quality scoring standard, which can assign corresponding scores by judging the proximity of the subgraph structure and community definition; then use algorithms such as greedy/distributed iteration to search for every possible community in the network Divide, record and output the division result with the highest score. At present, many community quality functions have been proposed, among which the most widely used is the modularity quality function, which defines the community score as the difference between the number of connections in the group and the expected number in the random network.

- Methods based on statistical inference

Another method that has attracted much attention in recent years is the community detection method based on statistical inference. This type of method regards the community as the main driving factor of the network structure, rather than an isolated feature, and believes that the connection probability between nodes is closely related to whether the communities they belong to are related, similar to people with similar interests in social networks. It is easier to generate links between them.

By utilizing probabilistic models such as the stochastic block model (SBM), statistical inference-based methods can use existing community partitions to calculate the probability of edge distribution among nodes, and then regenerate the link structure of the graph. This method believes that the higher the similarity between the graph structure regenerated in this way and the original graph structure, the higher the quality of community division.

- method based on random walk

Random walk can obtain the co-occurrence relationship between nodes in the graph by randomly jumping between nodes to detect the community structure in the graph. Since there are usually only sparse connections between network communities, the nodes to which they jump are often inside the same community, so this method can be used to merge different node groups from the bottom up to generate communities. The key to walking is the selection of the next hop node. Depending on the application scenario and data characteristics, different strategies are required for processing. Common walking strategies include uniform, frequency, and markov.

A nice property of this approach is that we don't need to actually perform any random walks to compute the information: an infinitely long random walk will converge to a closed expression for the entropy with a fixed probability value, which we can directly use as a quality function for community detection.

The disciplines and fields involved in the above methods are different. Due to space reasons, here is an excerpt of the Louvain algorithm - an optimization-based community discovery method for relatively detailed learning.

Part 03, Louvain - based on modularity optimization method 

As mentioned in the previous section, the optimization-based method needs to use the community quality function to evaluate the closeness of the subgraph structure and the community definition. At present, the most widely used quality function is modularity. The Louvain algorithm is based on the modularity. for community discovery. Therefore, we first briefly introduce the definition of modularity.

Newman et al. proposed the concept of modularity to measure the quality of community division. The formula is as follows:

Wherein 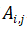represents the number of graph nodes 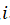and 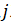edges between nodes, 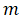represents the number of edges in the graph, 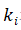represents 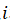the degree of nodes, and represents the expected value of the number of nodes and the number of edges between nodes and nodes when 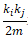the edges are randomly placed .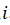

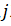
Therefore, modularity can be simply understood as: the ratio of edges in the community, minus the ratio of the expected number of edges in the community when the edges are randomly placed, divided by a constant value. If a community partition algorithm can divide as many densely connected points as possible into the same community and minimize the connections between communities, then a higher modularity score can be obtained.

The modularity of network division can be easily calculated through the following Python Demo:

import networkx as nx
# G1为原始图，G2为划分后的图，均用networkx.graph来表示
def Modularity(G1,G2):
    m=len(G1.edges())
    Aab=0
    Q=0.0
    for a in G1.nodes():
        for b in G1.nodes():
            if nx.has_path(G2,a,b):
                Aab=0
                if b in G1.neighbors(a):
                    Aab=1
                Q=Q+(Aab*m*2-nx.degree(G1,a)*nx.degree(G1,b))/(4*m*m)
    return Q
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.